2025

 

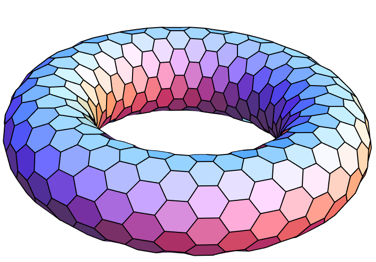
2025 = 3⁴ x 5²

quindi possiamo subito notare che 2025 è il quadrato di 3² x 5 = 45. L'ultimo anno quadrato è stato il 1936, anno in cui veniva presentata la Fiat 500 "Topolino", e Sepp Bradl era il primo uomo a superare i 100 metri nel salto con gli sci. Il prossimo anno quadrato sarà il 2116, millenario della conquista delle isole Baleari da parte di Pisa, e della morte di Arcimbaldo VI di Borbone.

2025 sarà un anno equidigitale, e quindi anche economico, come era stato il 2023, cioè si scrive con lo stesso numero di cifre (quattro) con cui si scrive la sua scomposizione in fattori primi.

Anche 2025, come tanti degli ultimi anni, sarà un numero di Harshad, traducibile come grande gioia, perché la somma delle su cifre (2 + 0 + 2 + 5 = 9) lo divide. Sarà anche apocalittico, perché 2²⁰²⁵ contiene le cifre 666.

A differenza degli anni recenti, invece, 2025 sarà un anno potente 💪, ovvero se un primo lo divide, allora lo divide anche quel primo al quadrato. In altre parole, tutti gli esponenti nella sua fattorizzazione in fattori primi devono essere maggiori di 1. L'ultimo anno potente è stato il 2000, anno di morte di  Klaus Wagner (famoso ad esempio per aver caratterizzato i grafi planari), e il prossimo sarà il 2048, che sarà anche una potenza di due.

Inoltre 2025:

• è 11111101001 in binario,
• è 3751 in ottale,
• è 7E9 in esadecimale,
• è MMXXIVI in numeri romani,
• in Unicode corrisponde alla lettera jona cha dell'alfabeto N'Ko: ߩ,
• è il 101-esimo anno piramidale pentagonale centrato. Ovvero, si può costruire una piramide di 2025 palline disposte su 101 piani, in cui ogni piano è un pentagono centrato con lato via via crescente. La piramide è instabile, perché ogni pallina è appoggiata su una pallina sottostante, e quindi rischia di cadere: meglio quindi costruirla con cilindri, anziché sfere!

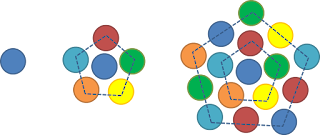I primi tre numeri pentagonali centrati: 1, 6 e 16. Formano i tre piani più alti della piramide pentagonale centrata.

Alcune ricorrenze che cadono nel 2025:

• 2⁵ = 32 anni fa, nel 1993, morivano Max August Zorn (matematico tedesco famoso per il lemma di Zorn) e Michele Sce (matematico italiano);
• 2⁶ = 64 anni fa, nel 1961, moriva Beppo Levi, matematico italiano;
• 2⁷ = 128 anni fa, nel 1897, moriva Karl Weierstrass, padre dell'analisi matematica moderna, e James Joseph Sylvester, famoso per i contribuiti nella teoria delle matrici;
• 100 anni fa, nel 1925, nascevano Giovanni Prodi, matematico italiano, e Harold Kuhn, matematico statunitense che insieme a Zermelo è noto per il teorema di Zermelo-Kuhn, secondo cui in un gioco a due giocatori, in cui questi muovono a turno e non c'entra la fortuna (come ad esempio gli scacchi, la dama, tris, ...), uno dei due ha una strategia vincente; inoltre morivano Felix Klein, da cui prende il nome la bottiglia di Klein, e Gottlob Frege, padre della moderna logica matematica.

Buon 1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ ! 🍸

Biscotti matematici

In queste vacanze di Natale 🎄, perché non fare qualche biscotto matematico? 🍪 

I biscotti possono essere di qualunque forma, e quindi anche poligonali.

Se hai una stampante 3d, puoi scaricare i file degli stampi che ho utilizzato per fare questi biscotti (fai attenzione ad utilizzare un materiale adatto al contatto alimentare, e informati sui rischi di utilizzare oggetti stampati in 3d a contatto con gli alimenti): contengono un triangolo, un pentagono, un ottagono e un decagono con lato 3cm, e un triangolo, un quadrato, un pentagono ed un esagono con lato 5cm.

Oppure scarica il file python per generare stampi poligonali con le tue caratteristiche preferite!

Questi biscotti sono ottimi da mangiare durante una tombola dei poliedri, ma si prestano anche ad altre attività: con quali poligoni riesci a tassellare il piano, e quindi a sfruttare al meglio tutta la pasta stesa? Quali figure puoi creare usando solo poligoni regolari? Quali sono le forme migliori da impilare per creare un alberello di Natale?

Con un po' di glassa ghiaccia reale, puoi anche provare a costruire qualche poliedro: i più facili sono probabilmente i prismi, ma, almeno teoricamente, si possono creare tutti i 120 numeri della mia tombola dei poliedri. Qual è il poliedro più complicato che riesci a costruire?

Buon Natale! 🎅

Halloween matematico 5

E' Halloween! 👻🎃💀

Gli anni scorsi vi ho proposto costumi da Versiera, the witch of Agnesi, da Scala del Diavolo, da Grim Reaper e da spettro di matrice. Quello di quest'anno è ottimo in coppia con uno spettro di matrice: il 

teorema spettrale

Il teorema spettrale dice che:

Ho già parlato di matrici nel post di Halloween dell'anno scorso, qui.

Una matrice simmetrica è una matrice che rimane uguale se la ribalti lungo la sua diagonale.

Una matrice diagonale è una matrice che ha numeri diversi da zero solo lungo la sua diagonale.

Una matrice ortogonale è una matrice che specchiata lungo la diagonale e poi moltiplicata per se stessa diventa l'identità; è una proprietà molto utile in matematica.

Il teorema spettrale ci dice che, per qualunque matrice simmetrica (con numeri reali) scegliamo, possiamo trovare una matrice ortogonale che la faccia diventare una matrice diagonale.

Polyhedra and hexagons

[Questo post è in inglese. Leggi qui la versione italiana]

The most well-known polyhedra, fo sure, are the regular ones, also called platonic: tetrahedra, octahedra, cubes, icosahedra, and dodecahedrons.

They are made of triangles, squares and pentagons... But can we make one out of hexagons?

The answer is no, at least if we want them to be equal and regular. This follows from the fact that putting three hexagons side by side, takes up the whole 360° angle (120° each one), and we can't bend them to make something three-dimensional.

The triangles take up the whole angle too, but we need six of them to do it. So, with only three, four or five we can create polyhedra: the tetrahedron, the octahedron and the icosahedron respectively.

What if we settle to only have some faces that are hexagons? In this case, we can construct polyhedra. For example, using pentagons, we can make a truncated icosahedron, which is the football's ball.

But let's suppose that we want all the faces to be hexagons.

Maybe it suffices to take them not regular? For example, there exists only one polyhedron made of squares (that is, regular quadrilaterals): the cube; but, if we don't ask them to be regular, there are others, one of them is the rhombic icosahedron. Then, maybe, there are no polyhedra made of regular hexagons, but there are made of irregular ones.

The answer, sadly, is always no!

Using Euler's formula for polyhedra, that says

vertices + faces = edges + 2 ,

(that is, the number of vertices, added to the number of faces, is equal to the number of edges plus two) one can prove that you can't construct a polyhedron made only of hexagons, it doesn't matter if regular or not!

This is very sad news for polyhedra and hexagons lovers :(

But don't worry! Nothing is over!

Euler's formula is only true for polyhedra that are "balls", which means that they have no holes. But Euler's formula for donut-polyhedra is different:

vertices + faces = edges .

Thus, we can present a polyhedron made only of hexagons! Ladys and gentelmans... the Szilassi's polyhedron!

It has seven faces, all hexagonal. Each face has six edges and thus touches all the other faces. Six of those faces are concave hexagons, equal in pairs. The last one is a convex hexagon, the only one, and it is "in the hole".

This is its net:

Unfortunately, someone may say that concave hexagons are ugly.

I disagree. But, for those people, we'll search if it is possible to have a polyhedron made only of convex hexagons.

Searching on the internet, one can find this picture: a donut polyhedron exactly as we search it.

But... there is something wrong. This polyhedron can't exist! This is why:

We say that our polyhedron has n hexagonal faces.

Then, its edges are 3n, because every face has 6 edges, and every edge belongs to two faces.

Take now Euler's formula for donut polyhedra: vertices + faces = edges, then, soubstituting faces = n and edges = 3n, we obtain vertices = 2n.

Every face has 6 vertices, so every vertex must belong (on average) to 3 faces (it's the same argument as made before with edges). But, in a vertex, we can't have less than 3 faces, that is the same thing as saying: a vertex can't belong to less than 3 faces.

Thus, in every vertex, there are exactly 3 faces.

(Note: this is true for Szilassi's polyhedron, which is an example of a donut polyhedron with hexagonal faces)

We'll see now that, if the faces are convex hexagons, this is impossible!

The sum of the angles of a (convex) hexagon is 6x120°. Thus, each angle of each hexagon is, on average, 120°, thus, each vertex, on average, has a total of 3x120° = 360°. 

Here is the problem: if I have three faces that meet in a vertex and their angles are less than 180° (because the hexagons are convex), then the total sum of these angles can't be more or equal than 360°. This is true for every polyhedron you can think of (this is not a proof, but if you want to convince yourself try moving the points A, B and C here, and watch how the angle sum change); and one can prove it without too much trouble, but I will not do it here.

This means that in all the vertices, there are less than 360°, which is in contradiction with what was said before: on average, there are 360°. 

Having a contradiction, a donut polyhedron made only of convex hexagons (as the one in the picture) cannot exist...

 ❒

So, the picture found on the internet is trying to fool us: probably, the hexagons on the inside are not planar, but we can't see it from far away.

Let us return to our initial question: can we find a polyhedron made only of convex hexagons? The answer is no if it is a sphere (for Euler's formula) and no again if it is a donut, but maybe, adding holes to our donut... Maybe!

(Note: when I say "maybe", I really mean it! As far as I know, this is an open question in math: nobody knows the answer.)

Poliedri ed esagoni

[This post is in italian. Read here the English version]

I poliedri più conosciuti sono sicuramente quelli regolari, anche detti platonici: tetraedri, ottaedri, cubi, icosaedri e dodecaedri.

Sono fatti di triangoli, quadrati e pentagoni... Ma possiamo farne di esagoni?

La risposta è no, quantomeno se li vogliamo tutti uguali tra loro e regolari. Questo perché se affianchiamo tre esagoni questi riempiono tutto l'angolo di 360° (120° ciascuno) e non riusciamo a piegarli per creare qualcosa di tridimensionale. 

Anche i triangoli riempiono tutto l'angolo, ma per fare questo dobbiamo usarne sei. E quindi affiancandone solo tre, quattro o cinque riusciamo a creare poliedri: il tetraedro, l'ottaedro e l'icosaedro rispettivamente.

E se ci accontentiamo che solo alcune facce siano esagoni? In tal caso riusciamo a costruire poliedri. Ad esempio, usando anche pentagoni, otteniamo un icosaedro troncato, ovvero la forma del pallone da calcio.

Ma supponiamo di volere per forza che tutte le facce siano esagoni.

Magari basta prenderli non regolari? Ad esempio, di poliedri fatti di quadrati (cioè quadrilateri regolari) ne esiste solo uno: il cubo; ma se non chiedo che siano regolari ne esistono altri, come l'icosaedro rombico. Quindi, magari, di poliedri fatti di esagoni regolari non ne esistono, ma con esagoni irregolari sì.

La risposta, purtroppo, è sempre no!

Usando la formula di Eulero per i poliedri, che ci dice che 

vertici + facce = lati + 2 , 

(cioè il numero di vertici, sommato al numero di facce, è uguale al numero di lati più due) si dimostra infatti che non si riesce a costruire un poliedro fatto solo di esagoni, non importa quanto irregolari siano!

Questa è proprio una pessima notizia per chi ama i poliedri e gli esagoni :(

Ma non disperate! Non tutto è perduto!

La formula di Eulero, infatti, vale solo per i poliedri che sono "palle", cioè che non hanno buchi. Ma per i poliedri a forma di ciambella la formula di Eulero è diversa: 

vertici + facce = lati .

Possiamo quindi presentare un poliedro fatto tutto di esagoni! Signori e signore, ecco a voi... il poliedro di Szilassi:

Ha sette facce, tutte esagonali. Ogni faccia ha sei lati, e dunque tocca tutte le altre facce. Sei di queste facce sono esagoni concavi, uguali a due a due. L'ultima faccia è un esagono convesso, l'unico, e si trova "nel buco".

Ecco il suo sviluppo:

Purtroppo, qualcuno potrebbe obiettare che gli esagoni concavi sono brutti.

Io non sono d'accordo, ma per queste persone cercheremo di capire se è possibile trovare un poliedro con solo facce esagonali convesse.

Cercando su internet si può trovare questa immagine: un poliedro fatto a ciambella proprio come lo vogliamo noi.

Eppure... qualcosa non torna. Questo poliedro in realtà non può esistere! Ecco perché:

Diciamo che il nostro poliedro ha n facce esagonali.

I suoi lati quindi sono 3n, perché ogni faccia ha 6 lati, ma ogni lato appartiene a due facce.

Prendiamo ora la formula di Eulero per i poliedri a ciambella: vertici + facce = lati, quindi, sostituendo facce = n e lati = 3n, otteniamo vertici = 2n.

Poiché ogni faccia ha 6 vertici, questo significa che ogni vertice deve appartenere (in media) a 3 facce (stesso ragionamento che avevamo fatto per contare i lati). Ma in un vertice non possono incontrarsi meno di 3 facce, che è la stessa cosa che dire: un vertice non può appartenere a meno di 3 facce.

Quindi in ogni vertice si incontrano esattamente 3 facce.

(Nota: in effetti, questo è vero per il poliedro di Szilassi, che è un esempio di poliedro a ciambella con sole facce esagonali)

Vedremo ora che, se le facce sono esagoni convessi, questo è impossibile!

La somma degli angoli di un esagono (convesso) è 6x120°. Quindi ogni angolo di ognuno dei nostri esagoni misura in media 120°, quindi in ogni vertice, in media, ho un totale di 3x120° = 360°. 

Il problema è qui: se ho tre facce che si incontrano in un vertice, e i loro angoli sono minori di 180° (perché gli esagoni sono convessi), la somma totale degli angoli non può essere maggiore o uguale a  360°. Questo è vero per tutti i poliedri a cui puoi pensare (non è una dimostrazione, ma se vuoi convincertene prova a spostare i punti A, B e C qui, e osserva come cambia la somma dei tre angoli); e si può dimostrare abbastanza facilmente, anche se non lo farò qui.

Questo vuol dire che in tutti i vertici ho meno di 360° totali, che contraddice ciò che avevamo detto prima: in media ho 360° totali.

Poiché abbiamo una contraddizione, un poliedro a ciambella con tutti esagoni regolari (come quello nella figura) non può esistere. 

 ❒

Insomma, l'immagine trovata su internet ci sta imbrogliando: probabilmente gli esagoni al suo interno non sono planari, sono curvi, ma da lontano non si vede.

Torniamo quindi alla nostra domanda iniziale: possiamo trovare un poliedro fatto di soli esagoni convessi? La risposta è no se è una sfera (per la formula di Eulero) e ancora no se è una ciambella, ma magari, aggiungendo buchi alla nostra ciambella... chissà!

(Nota: quando dico "chissà", intendo davvero chissà! Che io sappia, questo è un problema aperto in matematica: nessuno ne conosce la risposta.)

Dante e Fermat

Durante di Alighiero degli Alighieri, anche noto come Dante, nasce nel 1265 a Firenze, in Italia.

È considerato il padre della lingua italiana, e uno dei più grandi poeti e scrittori del nostro paese. Eppure, non era infallibile! 

Una dote importante per uno scrittore, infatti, è sicuramente saper riassumere, e dare ad ogni cosa il giusto spazio. Nel trentatreesimo canto del Purgatorio (versi 136-141), Dante ammette di aver sbagliato le misure:

S’io avessi, lettor, più lungo spazio 

da scrivere, i’ pur cantere’ in parte 

lo dolce ber che mai non m’avrìa sazio;

ma perché piene son tutte le carte 

ordite a questa cantica seconda, 

non mi lascia più ir lo fren de l’arte

🕮    🕮    🕮    🕮    🕮

Pierre de Fermat nasce nel 1601 a Beaumont-de-Lomagne, in Francia.

È uno dei più importanti matematici della storia (nonostante si occupasse della materia solo come hobby), ha dato importanti contributi allo sviluppo della matematica moderna e avuto scambi di lettere con molte altre importanti figure del suo tempo, come Mersenne e Pascal. Eppure, non era infallibile!

Mentre stava leggendo l'Arithmetica di Diofanto di Alessandria, scrisse sul bordo della pagina:

È impossibile separare un cubo in due cubi, o una potenza quarta in due potenze quarte, o in generale, tutte le potenze maggiori di 2 come somma della stessa potenza. Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina.

Quello che Fermat sostiene riguarda l'equazione

aⁿ + bⁿ = cⁿ

dove vogliamo che a, b e c siano numeri interi e positivi.

Se n=1, sappiamo trovare un sacco di terne di numeri a, b e c che soddisfano l'equazione: 1+2=3, 7+5=12, 2563+283646=286209 ...

Se n=2, queste terne si chiamano terne pitagoriche, e sono le possibili terne di lati dei triangoli rettangoli. Anche di queste sappiamo dimostrare che ne esistono infinite. Ad esempio: 3²+4²=5², 7²+12²=13² ...

Cosa succede per n=3 ? E per n=4 ? E per tutti gli altri possibili valori di n? Puoi provare quanto vuoi, ma, secondo Fermat, non esiste nessuna terna che soddisfi quell'equazione. Nessuna!

Eppure, Fermat non scrisse mai una dimostrazione di questo teorema, che venne chiamato "l'ultimo teorema di Fermat" (nonostante per essere davvero un teorema avrebbe dovuto avere una dimostrazione).

Lo dimostrò nel caso di n=4, e poi molti altri matematici dopo di lui provarono a dimostrarlo per altri valori di n. Eulero lo dimostrò per n=3, Dirichlet e Legendre per n=5, Gabriel Lamé per n=7.

Finalmente, nel 1994, Andrew Wiles è riuscito a dimostrarlo per tutti i possibili valori di n.

Ma che fine ha fatto la dimostrazione che Fermat sosteneva di avere in quel margine di pagina?

Ovviamente, c'è la possibilità che avesse davvero una dimostrazione del teorema, ma si tende ad escludere questa ipotesi: la dimostrazione di Wiles utilizza metodi matematici molto recenti, che Fermat non aveva, ed è impossibile che li avesse sviluppati da solo, e senza farne parola con nessuno! È possibile che avesse una dimostrazione più semplice, che usava solo strumenti matematici in suo possesso? Anche questo è difficile: in 400 anni, con tutte le persone che hanno provato a risolvere il problema, qualcuno l'avrebbe trovata!

L'ipotesi più accreditata è che Fermat avesse una dimostrazione, ma che questa contenesse un errore. Errore di cui, forse, anche lui si era accorto (ma dopo la famosa annotazione a margine di pagina): questo spiegherebbe perché non l'abbia mai pubblicata o scritta a nessuno, neanche quando poi ha reso nota la sua dimostrazione nel caso particolare in cui n=4.

Ma c'è una terza ipotesi: e se Fermat avesse deciso di fare uno scherzo alle generazioni future? Se avesse scelto una congettura volutamente difficile, sperando che più persone possibile ci sbattessero la testa, cercando la sua dimostrazione, che in realtà non esisteva?

Per quanto mi riguarda, mi piace immaginare Fermat nel suo studio, la scrivania piena di fogli, i mobili di legno massiccio, le nuvole fuori dalla finestra; una copia della Commedia di Dante poggiata sulla poltrona, aperta all'ultima pagina del Purgatorio; e lui che scrive con una penna d'oca quell'annotazione a margine, mentre se la ride.

Buon Pi Greco Day!

 Oggi è il 14 marzo, il giorno del Pi Greco!

Il Pi Greco è probabilmente la costante matematica più conosciuta, quel numero che si nasconde nel cerchio e da vita a numerose competizioni per ricordarne le cifre.

Vuoi saperne di più? Qui trovi il mio post di qualche anno fa.

Buon Pi Day!

2024

2024 = 2³ ⨯ 11 ⨯ 23

quindi possiamo calcolare la somma dei suoi divisori:

1 + 2 + 4 + 8 + 11 + 22 + 44 + 88 + 23 + 46 + 92 + 184 + 253 + 506 + 1012 + 2024 =

= (1 + 2 + 4 + 8) ⨯ (1 + 11) ⨯ (1 + 23) =

= 15 ⨯ 12 ⨯ 24 = 4320

Non è un evento che capita spesso! L'ultimo anno con somma dei divisori 4320 è stato il 1938, anno in cui l'Italia vince il suo secondo mondiale di calcio ⚽. Ma per fortuna non dovremo aspettare molto per il prossimo: dopo il 2024, infatti, anche il 2030 avrà 4320 come somma dei suoi divisori.

Il 2024 sarà un anno stravagante😵, come lo erano il 2022 e il 2021, perché per scriverlo in fattori primi si usano cinque cifre, contro le quattro che servono normalmente.

Il 2024 non sarà un anno perfetto, ma sarà semiperfetto🥈: i numeri semiperfetti sono quelli che si possono scrivere come somma di alcuni dei suoi divisori. Ad esempio, se eliminiamo 88, 184 e 2024 dalla somma, otteniamo 1 + 2 + 4 + 8 + 11 + 22 + 44 + 23 + 46 + 92 + 253 + 506 + 1012 = 2024.

Il 2024 è un numero di Harshad (d'altra parte, lo erano anche il 2023, il 2022 e il 2020), ovvero la somma delle sue cifre (8) lo divide; il termine "Harshad" deriva dal sanscrito "harşa", che significa "grande gioia"😀.

Il 2024 sarà un anno apocalittico👿, perché la scrittura decimale di 2²⁰²⁴ contiene le cifre 666. Ma, come ho scritto nel 2021, gli anni apocalittici sono davvero tanti!

Il 2024 sarà un anno intoccabile🔥: cioè non esiste nessun intero che abbia come somma dei suoi divisori propri 2024.

Il 2024, inoltre, sarà un anno pratico🔨! Questo significa che tutti i numeri minori di 2024 possono essere scritti come somma di suoi divisori. Qualche esempio:

• 1 = 1
• 2 = 2
• 3 = 2 + 1
• 4 = 4
• 5 = 4 + 1
• 6 = 4 + 2
• 7 = 4 + 2 + 1
• 8 = 8
• 9 = 8 + 1
• ...
• 1789 = 1012 + 506 + 253 + 13 + 4 + 1
• 1790 = 1012 + 506 + 253 + 13 + 4 + 2
• ...
• 2022 = 1012 + 506 + 253 + 92 + 46 + 44 + 23 + 22 + 11 + 8 + 4 + 1
• 2023 = 1012 + 506 + 253 + 92 + 46 + 44 + 23 + 22 + 11 + 8 + 4 + 2

2024 è anche il numero di braccialetti di 3 perline diversi che si possono fare se si hanno a disposizione 22 colori. Infatti:

• se scegliamo tre perline tutte dello stesso colore, possiamo fare 22 braccialetti diversi: uno per ogni colore;
• se scegliamo due perline dello stesso colore, e la terza di un colore diverso, possiamo fare 22 ⨯ 21 = 462 braccialetti;
• se scegliamo tre perline di tre colori diversi, possiamo fare 22 ⨯ 21 ⨯ 20 / 6 = 1540 braccialetti.

Quindi in tutto possiamo fare 22 + 462 + 1540 = 2024 braccialetti diversi.

Inoltre 2024 :

• è 11111101000 in binario,
• è 3750 in ottale,
• è 7E8 in esadecimale,
• è MMXXIV in numeri romani (e non solo! Si può scrivere anche utilizzando gli stessi simboli, ma con qualche operazione in più: (X / V) ^X ⨯ I ^M + M = (10 / 5) ^10 ⨯ 1 ^ 1000 + 1000 = 2024),
• in Unicode corrisponde alla lettera jona ja dell'alfabeto N'Ko: ߨ ,
• è il ventiduesimo numero tetraedrico. Ovvero, se si costruisce un tetraedro di 22 palline di lato, serviranno in tutto 2024 palline.

Alcune ricorrenze che cadono nel 2024:

• 2⁵ = 32 anni fa, nel 1992, moriva Grace Murray Hopper, matematica statunitense, una pioniera della programmazione informatica;
• 2⁶ = 64 anni fa, nel 1960, morivano John Henry Constantine Whitehead, matematico britannico,  Oswald Veblen, matematico statunitense, colui che dimostrò formalmente il teorema della curva di Jordan, e Eric Temple Bell, matematico scozzese;
• 2⁷ = 128 anni fa, nel 1896, nascevano Wilhelm Ackermann, matematico tedesco, e Pavel Sergeevič Aleksandrov, matematico sovietico;
• 2⁸ = 256 anni fa, nel 1768, nasceva Jean Baptiste Joseph Fourier, quello della serie e della trasformata di Fourier;
• 2⁹ = 512 anni fa, nel 1512, nasceva Gerardo Mercatore, che inventò la proiezione di Mercatore, caratterizzata dal mantenere gli angoli corretti;
• 100 anni fa, nel 1924, moriva Helge von Koch, colui che da il nome alla curva di Koch, un frattale.

Buon (X / V) ^X  ⨯ I ^M + M !

Addobbi matematici per Natale

Uno degli addobbi più comuni sui nostri alberi 🎄 sono le palle di Natale.

Per la maggior parte, si tratta, in realtà, di sfere. Ovvero non sono palle piene (peserebbero troppo!) ma solo l'involucro esterno a forma di sfera.

In matematica, e più in particolare in topologia, la sfera è una superficie, una della più semplici. Allora perché non aggiungere all'albero anche altre superfici?

Ad esempio, un toro (il nome matematico della superficie di una ciambella).

O possiamo aggiungere altri buchi alla superficie. La sfera non ne ha, il toro ne ha uno, possiamo farne due.

 E ovviamente possiamo continuare quanto vogliamo...

Qual è l'addobbo più matematico sul tuo albero di Natale?

Halloween matematico 4

E' Halloween! 👻🎃💀

Dopo le maschere da Versiera, the witch of Agnesi, da Scala del Diavolo e da Grim Reaper degli anni scorsi, quest'anno vi propongo un nuovo costume a tema matematica: uno spettro 👻 (di matrice).

Necessario:

• una matrice;
• dei biscotti 🍪;
• un lenzuolo bianco;
• colla.

Preparazione:

Come prima cosa devi scegliere la tua matrice preferita.

Cos'è una matrice? È un quadrato pieno di numeri, un oggetto molto importante in matematica. Ecco alcune matrici:

Per questo tutorial prenderemo lei:

Il cibo preferito delle matrici sono i vettori, delle colonne di numeri. 

Le matrici sono come delle macchinette che si mangiano un vettore e ne sputano fuori un altro. In matematica diciamo che moltiplicando una matrice per un vettore otteniamo un altro vettore. Se sei curioso puoi approfondire l'argomento qui. Ma non è quello di cui stavamo parlando.

A volte, dando ad una matrice un certo vettore, questa sputa fuori lo stesso vettore, o un multiplo di quel vettore. Ad esempio 2 volte quel vettore. In questo caso diciamo che 2 è un autovalore della matrice.

Più la matrice è grande, più autovalori ha. Ad esempio una matrice di tre righe ha tre autovalori, una matrice di 100 righe ne ha 100.

Gli autovalori sono numeri molto importanti per le matrici, ma può essere molto difficili trovarli. Il modo migliore è probabilmente offrendo in cambio dei biscotti, ed è quello che ti consiglio di fare (in alternativa puoi usare questo sito).

Io sono riuscita a farmi dare gli autovalori dalla mia matrice:

Quindi, cos'è uno spettro? È semplicemente l'insieme degli autovalori di una matrice.

Una volta ottenuti gli autovalori della tua matrice, quindi, ti basta attaccarli sul lenzuolo bianco usando un po' di colla, per completare il tuo vestito da spettro 👻.

Quando non è Halloween...

Le matrici e i loro autovalori sono oggetti molto importanti in matematica. Anche lontano da Halloween, quindi, può essere utile avere sempre a portata di mano lo spettro della tua matrice preferita.

Ecco le istruzioni per farne uno all'uncinetto:

Legenda:

sc : maglia bassa (single crochet)

sc inc : incremento (due maglie basse nello stesso punto)

sc dec : decremento (una maglia bassa lavorata su due punti)

dc : maglia alta (double crochet)

sl st : maglia bassissima (slip stitch)

Istruzioni:

Lavora in circolo.

Riga 1: 6 sc in un magic ring (in tutto 6 maglie)

Riga 2: sc inc x6 (in tutto 12 maglie)

Riga 3: [sc x3, sc inc] x3 (in tutto 15)

Riga 4: [sc x2, sc inc, sc x2] x3 (18)

Righe da 5 a 7: sc x18 (18)

Riga 8: [sc x2, sc dec, sc x2] x3 (15)

Riga 9: sc x15 (15)

Riga 10: [sc x4, sc inc] x3 (18)

Righe da 11 a 13: sc x18 (18)

Riga 14: [sc x2, sc inc, sc x3] x3 (21)

Riga 15: [sc e dc lavorate nello stesso punto, sc, sl st] x7 (28)

Scuola guida per matematici: Attenzione Caduta Esagoni

Uscendo di casa è facile incontrare cartelli stradali.

E i cartelli stradali hanno un legame con la matematica: come in questa disciplina si utilizzano +, -, ⅀, ⊥, ⟹..., così anche la segnaletica stradale serve per comunicare velocemente e brevemente con gli altri.

A volte, però, il significato matematico dei segnali non è lo stesso che i comuni utenti della strada gli attribuiscono. Ad esempio...

Attenzione: Caduta Esagoni

Il cartello viene usato per segnalare un tratto di strada dove esiste pericolo per la caduta di esagoni, o l'eventuale presenza dei medesimi sulla carreggiata. 

Il simbolo ha la scarpata o pendice a destra o a sinistra a seconda che le stesse siano a destra o a sinistra rispettivamente.

Ma da dove deriva questo rischio? Perché gli esagoni dovrebbero cadere sulla strada?

2023

 2023 = 7 × 17²

ed una delle prime cose di cui ci si accorge è che tutti i suoi fattori primi finiscono con la cifra 7. Potremmo chiederci quanto spesso succede, e facendo qualche conto scopriremmo che, a partire dall'anno 0, il 2023 è il 23-esimo anno con questa proprietà se non teniamo conto dei numeri primi (l'ultimo era stato il 1939  = 7 × 277), ed il 105-esimo (105 è divisibile per 7 !) se contiamo anche i primi (in questo caso dal 1939 ad ora ci sono stati anche il 1987, il 1997 e il 2017).

2023 è un anno equidigitale, cioè sono necessarie lo stesso numero di cifre per scriverlo (4) che per scrivere la sua fattorizzazione (1+2+1). Questo lo rende anche un numero economico 💸, ovvero non stravagante (i numeri stravaganti sono quelli per cui la fattorizzazione richiede più cifre).

2023 sarà un anno fortunato 🍀! L'ultimo era stato il 2019, puoi leggere il post di quell'anno per scoprire cosa significa.

Come l'anno scorso questo sarà un anno di Harshad, termine che deriva dal sanscrito "harşa" e che si può tradurre come "grande gioia" 😀. I numeri di Harshad sono quelli la cui somma delle cifre (in questo caso 2+0+2+3=7) divide il numero stesso.

2023 può essere scritto in un unico modo come somma di una potenza di 2 e di un numero primo, è infatti 2023 = 512 + 1511 = 2⁹ + 1511.

2023 è un anno congruente: ovvero è l'area di un triangolo rettangolo con cateti e ipotenusa che sono numeri razionali. In particolare 595/12, 408/5 e 5729/60.

Qualche altro modo per scrivere 2023:

• è 11111100111 in binario;
• è 3747 in ottale;
• è 7E7 in esadecimale;
• è MMXXIII in numeri romani;
• in Unicode corrisponde alla lettera Nya Woloso dell'alfabeto N'Ko: ߧ.

Alcune ricorrenze che cadono nel 2023:

• 2⁶ = 64 anni fa, nel 1959:
• moriva Renato Caccioppoli, matematico italiano che contribuì alla risoluzione del diciannovesimo problema di Hilbert, e che era solito passeggiare portando al guinzaglio un gallo 🐓;
• si svolgono in Romania le prime Olimpiadi Internazionali della Matematica, con la partecipazione di 7 nazioni.
• 100 anni fa, nel 1923: 
• moriva Johannes Diderik van der Waals, premio Nobel per la fisica; 
• moriva John Venn, l'inventore dei diagrammi di Eulero-Venn; 
• moriva Hertha Marks Ayrton, prima donna ad ottenere diversi riconoscimenti in campo scientifico.
• 2⁷ = 128 anni fa, nel 1895: 
• nasceva Alexander Aitken, matematico neozelandese e calcolatore prodigio. Ad esempio riuscì a calcolare in soli trenta secondi il risultato della moltiplicazione 987 654 321 × 123 456 789; 
• nasceva Júlio César de Melo e Sousa, matematico e scrittore brasiliano conosciuto con lo pseudonimo di Malba Tahan, l'autore del libro L'uomo che sapeva contare; 
• nasceva Rolf Nevanlinna, matematico finlandese a cui è stato dedicato il premio Nevanlinna;
• moriva Ludwig Schläfli, matematico svizzero che ha introdotto gli spazi a più dimensioni e i politopi (i poliedri in più dimensioni).

Buon 2⁹ + 1511 ! 🌠

Tombola dei poliedri

Il Natale si avvicina! Quest'anno al posto della solita Tombola puoi provare questa tombola dei Poliedri.

Come funziona?
Esattamente come una normale tombola, ma con 120 numeri. Anziché da 1 a 90, si estraggono numeri da 0 a 119. Ad ogni numero è associato un poliedro.

Come si vince?
Ogni cartella contiene 20 numeri anziché 15, cinque per riga, su quattro righe. Oltre ai premi classici della tombola (ambo, terna, quaterna, cinquina e tombola), puoi vincere qualcosa anche con:

• doppia cinquina: due cinquine completate nella stessa cartella;
• tripla cinquina: tre cinquine completate nella stessa cartella;
• quaterna verticale: ogni cartella contiene una colonna con quattro poliedri, che se completata fa vincere questo premio;
• terna verticale: ogni cartella contiene una colonna con tre poliedri (La terna verticale non può essere fatta sulla colonna da quattro!);
• ambo verticale: ogni cartella contiene tre colonne con due poliedri (l'ambo verticale non può essere fatto sulle colonne da tre o quattro);
• mono verticale: ogni cartella contiene 7 colonne con un solo poliedro (di nuovo, il mono verticale non può essere fatto sulle colonne da due, tre o quattro). Questo premio viene solitamente assegnato molto presto!
• ambo verticale totale: se si completano tutte le colonne da due di una cartella;
• mono verticale totale: se si completano tutte le colonne da uno di una cartella.

Posso saperne di più sui poliedri?
Ovviamente!
I 120 poliedri presenti in questa tombola hanno tutte le facce che sono poligoni regolari. Sono inoltre non intrecciati, ovvero le facce non si intersecano tra di loro (alcuni esempi di poliedri intrecciati? I poliedri di Keplero-Poinsot).
In particolare possiamo dividerli in quattro categorie:

• i poliedri regolari o platonici sono i primi cinque della lista, nonché i più conosciuti: tetraedro, cubo, ottaedro, dodecaedro ed icosaedro. Sono gli unici cinque ad avere tutte le facce uguali tra di loro, e che si incontrano nello stesso numero in ogni vertice (pagina wikipedia);
• i poliedri semiregolari o archimedei sono tredici (senza contare prismi e antiprismi). Compaiono se rilassiamo un po' le condizioni imposte ai poliedri platonici: chiediamo comunque che ogni vertice sia uguale agli altri, ma consentiamo facce diverse (purché sempre regolari!). Qui troviamo, tra gli altri, l'icosaedro troncato: la forma più famosa del pallone da calcio (pagina wikipedia);
• i prismi hanno due basi uguali (ognuna con n lati), unite da una corona di n quadrati. I prismi sarebbero in numero infinito, ma in questa tombola sono stati inclusi solo quelli con base triangolare, quadrata (che in realtà è un cubo), pentagonale, esagonale, ottagonale e decagonale (pagina wikipedia);
• gli antiprismi hanno due basi uguali (ognuna con n lati), unite da una corona di 2 n triangoli. Anche gli antiprismi sarebbero in numero infinito, e sono stati inclusi solo quelli con facce di base di 3 (in realtà l'ottaedro), 4, 5, 6, 8 o 10 lati (pagina wikipedia);
• i poliedri di Johnson sono 92 e comprendono tutti i poliedri non intrecciati con facce regolari che non rientrano nelle categorie precedenti. Tra questi la piramide quadrata e quella pentagonale, ma anche poliedri dai nomi esotici come il girobifastigio e l'ebesfenomegacorona (pagina wikipedia).

Cosa mi serve per giocare?
Per giocare puoi scaricare e stampare sei gruppi da sei cartelle ciascuno qui, il tabellone con tutte le immagini qui (puoi anche usare questo file per tagliare 120 quadrati, uno per ogni poliedro, ed usarli per estrarre i numeri) e la lista dei poliedri, associati al numero corrispondente, qui.

Per l'estrazione puoi utilizzare il programma qui sotto: clicca su "Estrai numero" per estrarre un numero e visualizzare il nome del poliedro corrispondente ed una sua immagine. È anche presente una tabella che si riempie automaticamente con il progredire dell'estrazione, per tenere traccia dei numeri già usciti. Per ricominciare da capo è sufficiente ricaricare la pagina.

Tutte le immagini, tranne quelle di prismi e antiprismi, ma compresa quella del prisma pentagonale, sono tratte da Wikipedia.
Nelle cartelle l'immagine di sfondo è una proiezione del 120-celle, uno dei sei poliedri regolari in quattro dimensioni, che ha 120 "facce" dodecaedriche.

Halloween matematico 3

E' Halloween! 👻🎃💀

Dopo le maschere da Versiera, the witch of Agnesi, e da Scala del Diavolo degli anni scorsi, quest'anno potete cambiare costume e travestirvi da Grim Reaper, il tristo mietitore.