Halloween matematico 2

E' Halloween! 👻🎃💀

Tre anni fa, nel 2018, pubblicavo questo post proponendo come costume di Halloween una maschera da Versiera, the witch of Agnesi.

Adesso potrete aggiungere un'altra maschera al vostro repertorio matematico: la scala del diavolo 😈.

La scala del diavolo, o scala di Cantor, è una funzione continua (cioè può essere disegnata "senza staccare la penna dal foglio").

Si tratta di un frattale, ovvero zoomando su una parte della scala, ci si ritrova davanti la scala stessa! Un altro esempio di frattale, molto legato a questa funzione, è l'insieme di Cantor.

😈

Come costruire la scala del diavolo 🔨

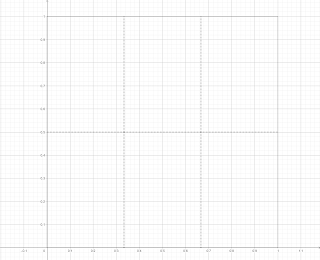
Per costruire la scala, partiamo da un quadrato di lato 1. La scala ci porterà dal punto (0,0) (l'origine) fino al punto (1,1). 

Dividiamo il quadrato in sei parti, come in figura:

Il primo scalino che costruiremo, che sarà lo scalino centrale della scala, si trova al centro della griglia che abbiamo appena disegnato. E' un segmento che va dal punto (1/3, 1/2) fino al punto (2/3, 1/2).

Adesso consideriamo il rettangolo in alto a destra e quello in basso a sinistra. Gli altri gradini della scala dovranno trovarsi in questi due settori.

In ogni settore ripetiamo quanto fatto nel quadrato iniziale: dividiamo il settore in una griglia 2x3 e tracciamo lo scalino centrale.

Adesso in ogni settore prendiamo il rettangolo in alto a destra e quello in basso a sinistra.

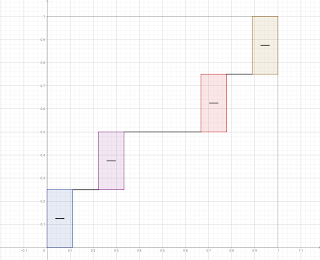
In ognuno di questi nuovi settori ripetiamo quanto appena fatto: dividiamo la griglia, tracciamo lo scalino centrale:

Dopo un altro passaggio:

Dobbiamo ripetere questa procedura all'infinito, ogni volta disegnando nuovi scalini sempre più corti.

Al primo passaggio disegniamo un gradino, al secondo 2, al terzo 4, poi 8 e così via, raddoppiando sempre. Alla fine ci ritroveremo con infiniti scalini, via via più corti sia in larghezza che in altezza.

Quella che otteniamo è la scala di Cantor, e benché possa non sembrare, è continua! Invece, è evidente che si tratta di un frattale, perché se facciamo lo zoom sul rettangolo in basso a sinistra (o su quello in alto a destra) troviamo la stessa scala da cui eravamo partiti (l'abbiamo costruita nello stesso modo).

Perché è importante?

Questa funzione ha alcune proprietà interessanti legate alla sua derivata (la derivata di una funzione in un punto ci dice quanto questa funzione stia crescendo. Così, se la funzione è piatta come su un gradino, la derivata è nulla. La derivata di una funzione però non esiste sempre).

Su ogni gradino la derivata è 0, mentre non esiste nei punti in cui "si cambia gradino", che corrispondono ai punti dell'insieme di Cantor.

Così ci troviamo ad avere una funzione debolmente crescente, che va da 0 ad 1 in modo continuo, senza salti, ma che non ha mai derivata positiva.

Che una cosa del genere possa esistere, se si ha dimestichezza con il concetto di derivata, risulta difficile da credere. Eppure, eccola qui. Anche per questo è detta "scala del diavolo", perché va contro la nostra intuizione.

Se vuoi saperne di più, questo articolo parla dell'argomento in modo più approfondito.

A proposito di Cantor

Georg Cantor, matematico vissuto a cavallo di 800 e 900, è famoso in particolare per il suo lavoro sulla teoria degli insiemi. Inizialmente questa non fu presa sul serio, ma più tardi David Hilbert la comparò al Paradiso.

Cantor ha quindi regalato ai matematici il Paradiso, ma anche la scala del diavolo.

Ho parlato di Cantor anche in questo post.

Colonna sonora

Ti stai chiedendo quale musica dovrebbe accompagnarti mentre entri trionfalmente alla tua festa di Halloween, indossando questa maschera?

Ecco due ottime scelte:

• The Devil's Staircase di Santa Clara Vanguard;
• Études, Libro 2: No. 13, L'escalier du diable di György Ligeti.