Il 14 marzo è il compleanno di Wacław Sierpiński (1882, 1969), Karl Wilhelm Lorenz (1886, 1918) e Michael Berry (1941), oltre che del famoso Albert Einstein (1879, 1955), ma non è per questo che è un giorno importante.
E' perché il 14 marzo è il pi greco day (che non è, come alcuni potrebbero pensare, il giorno di Pippo Ignazio).
Il pi greco è definito come il rapporto tra la circonferenza e il diametro di un cerchio. E' un numero decimale infinito. Non solo, è perfino irrazionale, nonché trascendente (cosa che rende impossibile la quadratura del cerchio, ma questa è un'altra storia).
 |
| Pippo Ignazio, originario di Atene, anche detto P. I. Greco. |
Approfondimento a fine pagina: Numeri trascendenti
Il pi greco day si festeggia il 14 marzo perché equivale a (circa) 3,14, che è proprio questa data scritta all'inglese "mese, giorno".
Certo, vista l'importanza che pi greco sembra avere (ha persino un giorno a lui dedicato!), viene da chiedersi quanto valga, quindi, pi greco.
Abbiamo detto che ha infinite cifre dopo la virgola, e che non si ripetono mai, ma quali sono queste cifre esattamente?
Qualcuno lo approssima a 22/7 (ovvero 3,142857 142857...), altri a 355/113 (ovvero 3,141592...), ma ovviamente nessuno di questi due numeri è esattamente pi greco.
Il fatto è che nessuno sa (né saprà mai) quanto vale pi greco esattamente.
Oh, sappiamo tante cose su di lui.
Sappiamo che la sequenza 0123456789 si trova al 17.387.594.880 decimale, ad esempio.
Sappiamo le sue prime 2 000.000.000.000.000 cifre (e anche oltre).
Approfondimento a fine pagina: Pi greco e approssimazione
Sappiamo anche come possiamo calcolare pi greco. All'inizio, questo conto veniva eseguito disegnando poligoni con un numero di lati molto alto, e che dunque approssimavano la circonferenza. Nel corso della storia, invece, i matematici hanno trovato diverse somme infinite uguali a pi greco (ovvero: se potessimo calcolare la somma di un numero infinito di addendi, otterremmo precisamente pi greco. Ma questo, per ovvie ragioni, ci è impossibile).
Una delle più complicate è probabilmente quella dei fratelli Chudnovsky:
Approfondimento a fine pagina: Calcolare questa sommatoria
E' bello poter calcolare pi greco... Ma non sono certo calcoli semplici! Per questo la ricerca di nuove cifre di questo numero, che ha destato interesse fin dall'antica Grecia, ha avuto un importante sviluppo con l'avvento dei computer. Si è passati da 1.120 cifre calcolate nel 1949 a più di 2.600.000.000.000 cifre calcolate nel 2010.
Eppure, non sappiamo tutto di pi greco. Non si è ancora riusciti a dimostrare, nonostante si suppone che sia vero, se pi greco sia un numero normale, né se sia un numero-universo.
Approfondimento a fine pagina: Numeri normali e numeri-universo
Resta comunque un'altra domanda da porsi su pi greco: perché è così famoso?
E' la costante matematica più citata, e chiunque, anche se non è un esperto, sa che è circa 3,14.
Ci sono persone che compongono odi o cucinano torte in suo onore; c'è chi ha speso una vita per calcolare le sue cifre, e chi le impara a memoria.
C'è persino un giorno dedicato a lui!
Ma perché?
Forse perché è allo stesso tempo un numero così semplice (se ne parla in quinta elementare) e così complicato (vi ricordate la sommatoria...?), nonché pieno di segreti.
Se si riuscisse a dimostrare che pi greco è normale e universale, se si trovasse una formula che permette di comprendere tutte le cifre di pi greco con pochi, semplici simboli, perderebbe il suo fascino? Oppure diventerebbe ancora più famoso?
Quanta bellezza in un rapporto così semplice come quello tra circonferenza e diametro!
Approfondimento: numeri decimali, irrazionali, trascendenti
Numeri decimali e irrazionali Un numero decimale è un numero che si scrive utilizzando la virgola. Ad esempio, sono decimali 2,5 e 0,0007.
Curiosi di sapere altri numeri trascendenti? Il più famoso, dopo pi greco, è il numero di Nepero: e. Sono trascendenti anche eℼ e uno tra e+ℼ e exℼ, anche se non si sa quale.
Un numero decimale può essere infinito se la sua rappresentazione decimale precisa è formata da infinite cifre dopo la virgola (ad esempio 1/3=0,33333...).
I numeri decimali infiniti possono essere periodici (ovvero le cifre si ripetono. Ad esempio 0,333... o 0,12 567 567 567...) oppure irrazionali (ovvero che non si possono scrivere come frazioni). Le cifre dopo la virgola dei numeri irrazionali, oltre ad essere infinite, non si ripetono con uno schema preciso. Ad esempio, radice di 2 è irrazionale.
Numeri trascendenti I numeri trascendenti sono numeri irrazionali che non possono essere espressi come soluzione di un'equazione a coefficienti razionali (i numeri razionali sono gli interi e le frazioni, anche negativi).
Radice di 2 non è trascendente, poiché è soluzione dell'equazione x2=2. Tutte le radici (e somme o differenze di radici) sono numeri non trascendenti. Al contrario, per quanto proviate, non riuscirete mai a trovare un'equazione a coefficienti razionali che ha come soluzione pi greco.
Pi greco e approssimazione 2 000.000.000.000.000 (o 2x1015) può sembrare solo un numero di 16 cifre (e cosa vuoi che sia 16?), ma in realtà è enorme. Solo per dare l'idea, se volessimo calcolare la circonferenza massima dell'universo visibile (supponendo che sia sferico e di conoscerne il raggio) con un'approssimazione minore del raggio di un atomo, ci basterebbero le prime 40 cifre.
2 000.000.000.000.000 è un numero 100.000.000.000.000 maggiore di 40.
Calcolare questa sommatoria Cerchiamo ora di capire, almeno approssimativamente, che cosa significano i simboli qui sopra.
Numeri normali e numeri-universo I numeri "normali" in base 10 sono numeri irrazionali in cui tutte le cifre compaiono con la stessa frequenza nel suo sviluppo in base 10, così come le coppie di cifre (00, 01, ... 98, 99), le triple (000, 001, ... 998, 999), ecc.
2 000.000.000.000.000 è un numero 100.000.000.000.000 maggiore di 40.
Calcolare questa sommatoria Cerchiamo ora di capire, almeno approssimativamente, che cosa significano i simboli qui sopra.
Per prima cosa, forse non sai che n!, che si legge "enne fattoriale", indica il prodotto di tutti i numeri da 1 a n. Quindi 1!=1, 2!=1x2=2, 5!=1x2x3x4x5=120, 10!=3.628.800. E' facile intuire che, se il numero n è grande, n! è molto grande. Pensa quindi quanto può diventare enorme (6xn)! quando n è solo "poco" grande.
Un'altra cosa che devi sapere è il significato del simbolo ∑, ovvero sommatoria. Significa che devi prima prendere n=0 (come scritto sotto) e calcolare quella frazione sostituendo n=0. Poi aumenti n di 1, e calcoli quella frazione sostituendo n=1. Poi aumenti n di 1, e calcoli quella frazione sostituendo n=2. E così via, fino ad arrivare ad infinito (come scritto sopra). Una volta che hai calcolato tutte le frazioni con tutti i valori di n, le sommi tra di loro (infatti è una sommatoria). Ovviamente non possiamo calcolare le frazioni per tutti gli n (perché sono infiniti). Più valori calcoliamo, e più quel numero si avvicina a 1/𝝅 (infatti all'inizio della frazione compare (-1)n , che è positivo per n pari e negativo per n dispari. Vuol dire che la frazione con n=0 sarà positiva, con n=1 negativa e così via. Aggiungendo e togliendo, piano piano ci avviciniamo alla meta). Facciamo un esempio. Per n=0 ottengo 0,0265258179936665073198830567197... Per n=1 ottengo -4,98422492211907170652852338404... x 10-16 Sommandoli ottengo 0,02652581799366600889739084481253... Moltiplicando per 12 ottengo 0,31830981592399210676869013775035... Questo valore equivale a 1/𝝅. Quindi 𝝅 = 3,1415933470263634335956928968... Ci è bastato calcolare due frazioni per ottenere un numero molto simile a 3,1415926535897932384626433... ma non sono affatto stati conti semplici!Numeri normali e numeri-universo I numeri "normali" in base 10 sono numeri irrazionali in cui tutte le cifre compaiono con la stessa frequenza nel suo sviluppo in base 10, così come le coppie di cifre (00, 01, ... 98, 99), le triple (000, 001, ... 998, 999), ecc.
I "numeri-universo" in base 10 sono numeri che nel loro sviluppo contengono qualunque sequenza immaginabile. Ad esempio, contengono la mia data di nascita, il tuo numero di cellulare e la sequenza di 1 e 0 con cui è salvato questo intero blog.
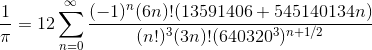
Nessun commento:
Posta un commento