Poliedri ed esagoni

[This post is in italian. Read here the English version]

I poliedri più conosciuti sono sicuramente quelli regolari, anche detti platonici: tetraedri, ottaedri, cubi, icosaedri e dodecaedri.

Sono fatti di triangoli, quadrati e pentagoni... Ma possiamo farne di esagoni?

La risposta è no, quantomeno se li vogliamo tutti uguali tra loro e regolari. Questo perché se affianchiamo tre esagoni questi riempiono tutto l'angolo di 360° (120° ciascuno) e non riusciamo a piegarli per creare qualcosa di tridimensionale. 

Anche i triangoli riempiono tutto l'angolo, ma per fare questo dobbiamo usarne sei. E quindi affiancandone solo tre, quattro o cinque riusciamo a creare poliedri: il tetraedro, l'ottaedro e l'icosaedro rispettivamente.

E se ci accontentiamo che solo alcune facce siano esagoni? In tal caso riusciamo a costruire poliedri. Ad esempio, usando anche pentagoni, otteniamo un icosaedro troncato, ovvero la forma del pallone da calcio.

Ma supponiamo di volere per forza che tutte le facce siano esagoni.

Magari basta prenderli non regolari? Ad esempio, di poliedri fatti di quadrati (cioè quadrilateri regolari) ne esiste solo uno: il cubo; ma se non chiedo che siano regolari ne esistono altri, come l'icosaedro rombico. Quindi, magari, di poliedri fatti di esagoni regolari non ne esistono, ma con esagoni irregolari sì.

La risposta, purtroppo, è sempre no!

Usando la formula di Eulero per i poliedri, che ci dice che 

vertici + facce = lati + 2 , 

(cioè il numero di vertici, sommato al numero di facce, è uguale al numero di lati più due) si dimostra infatti che non si riesce a costruire un poliedro fatto solo di esagoni, non importa quanto irregolari siano!

Questa è proprio una pessima notizia per chi ama i poliedri e gli esagoni :(

Ma non disperate! Non tutto è perduto!

La formula di Eulero, infatti, vale solo per i poliedri che sono "palle", cioè che non hanno buchi. Ma per i poliedri a forma di ciambella la formula di Eulero è diversa: 

vertici + facce = lati .

Possiamo quindi presentare un poliedro fatto tutto di esagoni! Signori e signore, ecco a voi... il poliedro di Szilassi:

Ha sette facce, tutte esagonali. Ogni faccia ha sei lati, e dunque tocca tutte le altre facce. Sei di queste facce sono esagoni concavi, uguali a due a due. L'ultima faccia è un esagono convesso, l'unico, e si trova "nel buco".

Ecco il suo sviluppo:

Purtroppo, qualcuno potrebbe obiettare che gli esagoni concavi sono brutti.

Io non sono d'accordo, ma per queste persone cercheremo di capire se è possibile trovare un poliedro con solo facce esagonali convesse.

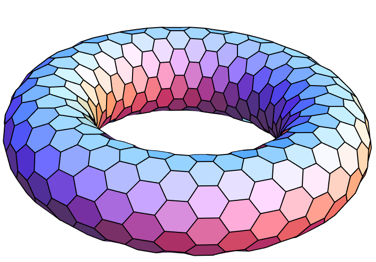
Cercando su internet si può trovare questa immagine: un poliedro fatto a ciambella proprio come lo vogliamo noi.

Eppure... qualcosa non torna. Questo poliedro in realtà non può esistere! Ecco perché:

Diciamo che il nostro poliedro ha n facce esagonali.

I suoi lati quindi sono 3n, perché ogni faccia ha 6 lati, ma ogni lato appartiene a due facce.

Prendiamo ora la formula di Eulero per i poliedri a ciambella: vertici + facce = lati, quindi, sostituendo facce = n e lati = 3n, otteniamo vertici = 2n.

Poiché ogni faccia ha 6 vertici, questo significa che ogni vertice deve appartenere (in media) a 3 facce (stesso ragionamento che avevamo fatto per contare i lati). Ma in un vertice non possono incontrarsi meno di 3 facce, che è la stessa cosa che dire: un vertice non può appartenere a meno di 3 facce.

Quindi in ogni vertice si incontrano esattamente 3 facce.

(Nota: in effetti, questo è vero per il poliedro di Szilassi, che è un esempio di poliedro a ciambella con sole facce esagonali)

Vedremo ora che, se le facce sono esagoni convessi, questo è impossibile!

La somma degli angoli di un esagono (convesso) è 6x120°. Quindi ogni angolo di ognuno dei nostri esagoni misura in media 120°, quindi in ogni vertice, in media, ho un totale di 3x120° = 360°. 

Il problema è qui: se ho tre facce che si incontrano in un vertice, e i loro angoli sono minori di 180° (perché gli esagoni sono convessi), la somma totale degli angoli non può essere maggiore o uguale a  360°. Questo è vero per tutti i poliedri a cui puoi pensare (non è una dimostrazione, ma se vuoi convincertene prova a spostare i punti A, B e C qui, e osserva come cambia la somma dei tre angoli); e si può dimostrare abbastanza facilmente, anche se non lo farò qui.

Questo vuol dire che in tutti i vertici ho meno di 360° totali, che contraddice ciò che avevamo detto prima: in media ho 360° totali.

Poiché abbiamo una contraddizione, un poliedro a ciambella con tutti esagoni regolari (come quello nella figura) non può esistere. 

 ❒

Insomma, l'immagine trovata su internet ci sta imbrogliando: probabilmente gli esagoni al suo interno non sono planari, sono curvi, ma da lontano non si vede.

Torniamo quindi alla nostra domanda iniziale: possiamo trovare un poliedro fatto di soli esagoni convessi? La risposta è no se è una sfera (per la formula di Eulero) e ancora no se è una ciambella, ma magari, aggiungendo buchi alla nostra ciambella... chissà!

(Nota: quando dico "chissà", intendo davvero chissà! Che io sappia, questo è un problema aperto in matematica: nessuno ne conosce la risposta.)