In queste vacanze di Natale 🎄, perché non fare qualche biscotto matematico? 🍪
I biscotti possono essere di qualunque forma, e quindi anche poligonali.
In queste vacanze di Natale 🎄, perché non fare qualche biscotto matematico? 🍪
I biscotti possono essere di qualunque forma, e quindi anche poligonali.
Oggi è la giornata nazionale degli Alberi! 🌳
Per festeggiare ecco qui uno schema del gioco logico Alberi. Trovi qui le regole, devi inserire 2 alberi in ogni riga, colonna e podere.
Sono uscite le informazioni per il dodicesimo Campionato Studentesco di Giochi Logici (per l'iscrizione, che deve essere effettuata dalle scuole, e per informazioni: www.puzzlefountain.com).
La finale si svolgerà sabato 5 aprile 2025, all'interno della Fiera Play, a Bologna.
Il primo allenamento online sarà a novembre: martedì 19 per primarie e medie, e mercoledì 20 per biennio e triennio.
I giochi da affrontare nelle categorie di primarie e medie saranno: Akari, Battaglia Navale, Caccia alle stelle, Camelot, Camping, Campo minato, Cioccolata, Facile come l'ABC, Futoshiki, Gravity, H2O, Hitori, Labirinto magico, Moonlighting, Nascondino, Nondango, Parquet, Percorso puntato, Tabelline e Vasi comunicanti.
Per biennio e triennio: Alberi, Buchi neri, Caccia alle stelle, Campo minato, Circuito chiuso, Doppio blocco, Facile come l'ABC, Fobidoshi, Freccia nera, Futoshiki, Grattacieli, Hakoiri, Heyawake, Labirinto magico, Nascondino, Parcheggio, Repulsione, Serpente a pois, Social Network e Yin Yang.
Puoi trovare esempi della maggior parte di questi giochi su questo blog, in questa pagina.
Alcuni giochi sono presenti per la prima volta nel Campionato:
Il 28 agosto di 140 anni fa, nel 1884, veniva scattata la prima foto di sempre ad un tornado. 🌪
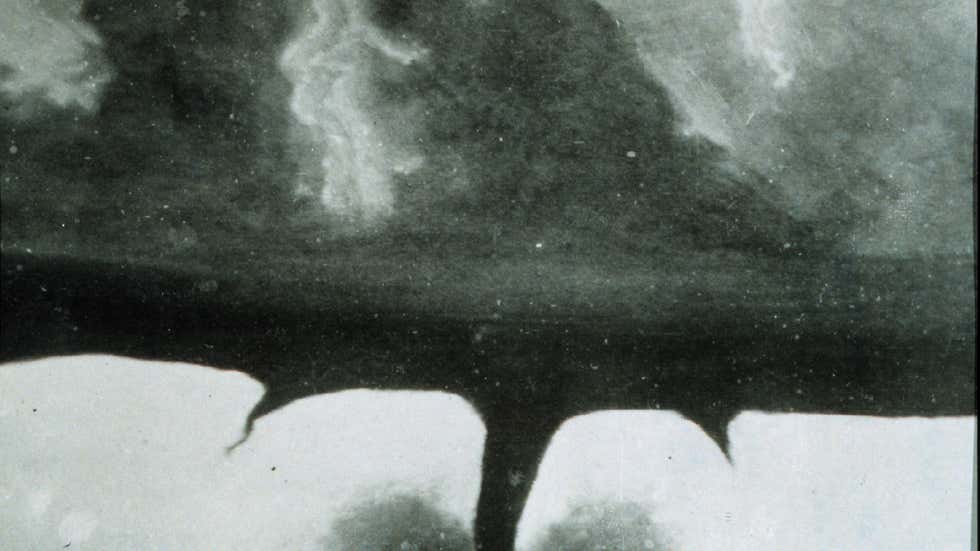 |
| Immagine da weather.com |
Per festeggiare questa occasione ecco qui due schemi di Ai quattro venti (regole).
(Nota: secondo altre fonti la prima foto di un tornado è un'altra, scattata il 26 aprile dello stesso anno)

[Questo post è in inglese. Leggi qui la versione italiana]
The most well-known polyhedra, fo sure, are the regular ones, also called platonic: tetrahedra, octahedra, cubes, icosahedra, and dodecahedrons.
They are made of triangles, squares and pentagons... But can we make one out of hexagons?
The answer is no, at least if we want them to be equal and regular. This follows from the fact that putting three hexagons side by side, takes up the whole 360° angle (120° each one), and we can't bend them to make something three-dimensional.
The triangles take up the whole angle too, but we need six of them to do it. So, with only three, four or five we can create polyhedra: the tetrahedron, the octahedron and the icosahedron respectively.
What if we settle to only have some faces that are hexagons? In this case, we can construct polyhedra. For example, using pentagons, we can make a truncated icosahedron, which is the football's ball.
But let's suppose that we want all the faces to be hexagons.
Maybe it suffices to take them not regular? For example, there exists only one polyhedron made of squares (that is, regular quadrilaterals): the cube; but, if we don't ask them to be regular, there are others, one of them is the rhombic icosahedron. Then, maybe, there are no polyhedra made of regular hexagons, but there are made of irregular ones.
The answer, sadly, is always no!
Using Euler's formula for polyhedra, that says
vertices + faces = edges + 2 ,
(that is, the number of vertices, added to the number of faces, is equal to the number of edges plus two) one can prove that you can't construct a polyhedron made only of hexagons, it doesn't matter if regular or not!
This is very sad news for polyhedra and hexagons lovers :(
But don't worry! Nothing is over!
Euler's formula is only true for polyhedra that are "balls", which means that they have no holes. But Euler's formula for donut-polyhedra is different:
vertices + faces = edges .
Thus, we can present a polyhedron made only of hexagons! Ladys and gentelmans... the Szilassi's polyhedron!
It has seven faces, all hexagonal. Each face has six edges and thus touches all the other faces. Six of those faces are concave hexagons, equal in pairs. The last one is a convex hexagon, the only one, and it is "in the hole".
This is its net:
Unfortunately, someone may say that concave hexagons are ugly.
I disagree. But, for those people, we'll search if it is possible to have a polyhedron made only of convex hexagons.
Searching on the internet, one can find this picture: a donut polyhedron exactly as we search it.
But... there is something wrong. This polyhedron can't exist! This is why:
We say that our polyhedron has n hexagonal faces.
Then, its edges are 3n, because every face has 6 edges, and every edge belongs to two faces.
Take now Euler's formula for donut polyhedra: vertices + faces = edges, then, soubstituting faces = n and edges = 3n, we obtain vertices = 2n.
Every face has 6 vertices, so every vertex must belong (on average) to 3 faces (it's the same argument as made before with edges). But, in a vertex, we can't have less than 3 faces, that is the same thing as saying: a vertex can't belong to less than 3 faces.
Thus, in every vertex, there are exactly 3 faces.
(Note: this is true for Szilassi's polyhedron, which is an example of a donut polyhedron with hexagonal faces)
We'll see now that, if the faces are convex hexagons, this is impossible!
The sum of the angles of a (convex) hexagon is 6x120°. Thus, each angle of each hexagon is, on average, 120°, thus, each vertex, on average, has a total of 3x120° = 360°.
Here is the problem: if I have three faces that meet in a vertex and their angles are less than 180° (because the hexagons are convex), then the total sum of these angles can't be more or equal than 360°. This is true for every polyhedron you can think of (this is not a proof, but if you want to convince yourself try moving the points A, B and C here, and watch how the angle sum change); and one can prove it without too much trouble, but I will not do it here.
This means that in all the vertices, there are less than 360°, which is in contradiction with what was said before: on average, there are 360°.
Having a contradiction, a donut polyhedron made only of convex hexagons (as the one in the picture) cannot exist...
❒
So, the picture found on the internet is trying to fool us: probably, the hexagons on the inside are not planar, but we can't see it from far away.
Let us return to our initial question: can we find a polyhedron made only of convex hexagons? The answer is no if it is a sphere (for Euler's formula) and no again if it is a donut, but maybe, adding holes to our donut... Maybe!
(Note: when I say "maybe", I really mean it! As far as I know, this is an open question in math: nobody knows the answer.)
[This post is in italian. Read here the English version]
I poliedri più conosciuti sono sicuramente quelli regolari, anche detti platonici: tetraedri, ottaedri, cubi, icosaedri e dodecaedri.
Sono fatti di triangoli, quadrati e pentagoni... Ma possiamo farne di esagoni?
La risposta è no, quantomeno se li vogliamo tutti uguali tra loro e regolari. Questo perché se affianchiamo tre esagoni questi riempiono tutto l'angolo di 360° (120° ciascuno) e non riusciamo a piegarli per creare qualcosa di tridimensionale.
Anche i triangoli riempiono tutto l'angolo, ma per fare questo dobbiamo usarne sei. E quindi affiancandone solo tre, quattro o cinque riusciamo a creare poliedri: il tetraedro, l'ottaedro e l'icosaedro rispettivamente.
La risposta, purtroppo, è sempre no!
Usando la formula di Eulero per i poliedri, che ci dice che
vertici + facce = lati + 2 ,
(cioè il numero di vertici, sommato al numero di facce, è uguale al numero di lati più due) si dimostra infatti che non si riesce a costruire un poliedro fatto solo di esagoni, non importa quanto irregolari siano!
Questa è proprio una pessima notizia per chi ama i poliedri e gli esagoni :(
Ma non disperate! Non tutto è perduto!
La formula di Eulero, infatti, vale solo per i poliedri che sono "palle", cioè che non hanno buchi. Ma per i poliedri a forma di ciambella la formula di Eulero è diversa:
vertici + facce = lati .
Possiamo quindi presentare un poliedro fatto tutto di esagoni! Signori e signore, ecco a voi... il poliedro di Szilassi:
Ha sette facce, tutte esagonali. Ogni faccia ha sei lati, e dunque tocca tutte le altre facce. Sei di queste facce sono esagoni concavi, uguali a due a due. L'ultima faccia è un esagono convesso, l'unico, e si trova "nel buco".
Ecco il suo sviluppo:
Purtroppo, qualcuno potrebbe obiettare che gli esagoni concavi sono brutti.
Io non sono d'accordo, ma per queste persone cercheremo di capire se è possibile trovare un poliedro con solo facce esagonali convesse.
Cercando su internet si può trovare questa immagine: un poliedro fatto a ciambella proprio come lo vogliamo noi.
Eppure... qualcosa non torna. Questo poliedro in realtà non può esistere! Ecco perché:
Diciamo che il nostro poliedro ha n facce esagonali.
I suoi lati quindi sono 3n, perché ogni faccia ha 6 lati, ma ogni lato appartiene a due facce.
Prendiamo ora la formula di Eulero per i poliedri a ciambella: vertici + facce = lati, quindi, sostituendo facce = n e lati = 3n, otteniamo vertici = 2n.
Poiché ogni faccia ha 6 vertici, questo significa che ogni vertice deve appartenere (in media) a 3 facce (stesso ragionamento che avevamo fatto per contare i lati). Ma in un vertice non possono incontrarsi meno di 3 facce, che è la stessa cosa che dire: un vertice non può appartenere a meno di 3 facce.
Quindi in ogni vertice si incontrano esattamente 3 facce.
(Nota: in effetti, questo è vero per il poliedro di Szilassi, che è un esempio di poliedro a ciambella con sole facce esagonali)
Vedremo ora che, se le facce sono esagoni convessi, questo è impossibile!
La somma degli angoli di un esagono (convesso) è 6x120°. Quindi ogni angolo di ognuno dei nostri esagoni misura in media 120°, quindi in ogni vertice, in media, ho un totale di 3x120° = 360°.
Il problema è qui: se ho tre facce che si incontrano in un vertice, e i loro angoli sono minori di 180° (perché gli esagoni sono convessi), la somma totale degli angoli non può essere maggiore o uguale a 360°. Questo è vero per tutti i poliedri a cui puoi pensare (non è una dimostrazione, ma se vuoi convincertene prova a spostare i punti A, B e C qui, e osserva come cambia la somma dei tre angoli); e si può dimostrare abbastanza facilmente, anche se non lo farò qui.
Questo vuol dire che in tutti i vertici ho meno di 360° totali, che contraddice ciò che avevamo detto prima: in media ho 360° totali.
Poiché abbiamo una contraddizione, un poliedro a ciambella con tutti esagoni regolari (come quello nella figura) non può esistere.
❒
Insomma, l'immagine trovata su internet ci sta imbrogliando: probabilmente gli esagoni al suo interno non sono planari, sono curvi, ma da lontano non si vede.
Torniamo quindi alla nostra domanda iniziale: possiamo trovare un poliedro fatto di soli esagoni convessi? La risposta è no se è una sfera (per la formula di Eulero) e ancora no se è una ciambella, ma magari, aggiungendo buchi alla nostra ciambella... chissà!
(Nota: quando dico "chissà", intendo davvero chissà! Che io sappia, questo è un problema aperto in matematica: nessuno ne conosce la risposta.)
Si è svolta oggi 18 maggio, sempre alla Polisportiva Sacca, la finale dell'undicesimo Campionato Studentesco di Giochi Logici.
Anche quest'anno i ragazzi della provincia di Massa-Carrara riescono a portare a casa numerosi premi.
Nella gara individuale riservata alle scuole medie, Massa-Carrara occupa tutte le posizioni pari premiate: al 6° posto Matteo Fusani, della Dazzi; al 4° e 2° posto Leonardo Zapponi e Giovanni Bengasi Fiorini 🥈 rispettivamente, dalla Taliercio, entrambi risolvendo correttamente tutti gli schemi della gara.
Nel biennio delle superiori la provincia (in particolare, il Marconi) occupa tutto il podio: al terzo posto Diego Barcellone 🥉, al secondo Francesco Manetti 🥈 e prima classificata Linda Babboni 🥇. Tutti e tre hanno risolto tutti i giochi proposti.
Per il triennio vengono premiati Tommaso Teani del Fermi al nono posto, Sara Galletti del Gentileschi al settimo posto, Andrea Borghini del Salvetti serale al sesto posto. Al primo posto a pari merito, con pochi secondi di differenza nella consegna e tutti gli esercizi risolti, Matteo Massa 🥇 del Marconi.
Nella gara a squadre delle scuole medie arrivano ottavi I gini, e quinti i LoGiCA, entrambe squadre della Taliercio.
Per il biennio a squadre, tutti i premiati sono di Massa-Carrara: arrivano sesti i Si dai cià del Marconi, quinti Gli armadilli fabriatici del Marconi, quarti I veri leoni del Zaccagna-Galilei, terzi le Barchette Luccicanti 🥉 del Marconi, secondi i Carboni Ardenti 🥈 del Rossi, e vincono i Persi in Labirinto Magico 🥇 del Fermi (Filippo Francini, Veronica Lucia, Giulia Mariotti e Emanuele Armanetti).
Nel trennio stravince, con più di 100 punti di distacco dai secondi classificati, Gli shocking rosacoleottero 🥇 del Marconi (Rosario Gentile, Sara Sigolo, Paolo Marino e Matteo Massa).

Durante di Alighiero degli Alighieri, anche noto come Dante, nasce nel 1265 a Firenze, in Italia.
È considerato il padre della lingua italiana, e uno dei più grandi poeti e scrittori del nostro paese. Eppure, non era infallibile!
Una dote importante per uno scrittore, infatti, è sicuramente saper riassumere, e dare ad ogni cosa il giusto spazio. Nel trentatreesimo canto del Purgatorio (versi 136-141), Dante ammette di aver sbagliato le misure:
S’io avessi, lettor, più lungo spazio
da scrivere, i’ pur cantere’ in parte
lo dolce ber che mai non m’avrìa sazio;
ma perché piene son tutte le carte
ordite a questa cantica seconda,
non mi lascia più ir lo fren de l’arte
🕮 🕮 🕮 🕮 🕮
Pierre de Fermat nasce nel 1601 a Beaumont-de-Lomagne, in Francia.
È uno dei più importanti matematici della storia (nonostante si occupasse della materia solo come hobby), ha dato importanti contributi allo sviluppo della matematica moderna e avuto scambi di lettere con molte altre importanti figure del suo tempo, come Mersenne e Pascal. Eppure, non era infallibile!
Mentre stava leggendo l'Arithmetica di Diofanto di Alessandria, scrisse sul bordo della pagina:
È impossibile separare un cubo in due cubi, o una potenza quarta in due potenze quarte, o in generale, tutte le potenze maggiori di 2 come somma della stessa potenza. Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina.
Quello che Fermat sostiene riguarda l'equazione
an + bn = cn
dove vogliamo che a, b e c siano numeri interi e positivi.
Se n=1, sappiamo trovare un sacco di terne di numeri a, b e c che soddisfano l'equazione: 1+2=3, 7+5=12, 2563+283646=286209 ...
Se n=2, queste terne si chiamano terne pitagoriche, e sono le possibili terne di lati dei triangoli rettangoli. Anche di queste sappiamo dimostrare che ne esistono infinite. Ad esempio: 3²+4²=5², 7²+12²=13² ...
Cosa succede per n=3 ? E per n=4 ? E per tutti gli altri possibili valori di n? Puoi provare quanto vuoi, ma, secondo Fermat, non esiste nessuna terna che soddisfi quell'equazione. Nessuna!
Eppure, Fermat non scrisse mai una dimostrazione di questo teorema, che venne chiamato "l'ultimo teorema di Fermat" (nonostante per essere davvero un teorema avrebbe dovuto avere una dimostrazione).
Lo dimostrò nel caso di n=4, e poi molti altri matematici dopo di lui provarono a dimostrarlo per altri valori di n. Eulero lo dimostrò per n=3, Dirichlet e Legendre per n=5, Gabriel Lamé per n=7.
Finalmente, nel 1994, Andrew Wiles è riuscito a dimostrarlo per tutti i possibili valori di n.
Ma che fine ha fatto la dimostrazione che Fermat sosteneva di avere in quel margine di pagina?
Ovviamente, c'è la possibilità che avesse davvero una dimostrazione del teorema, ma si tende ad escludere questa ipotesi: la dimostrazione di Wiles utilizza metodi matematici molto recenti, che Fermat non aveva, ed è impossibile che li avesse sviluppati da solo, e senza farne parola con nessuno! È possibile che avesse una dimostrazione più semplice, che usava solo strumenti matematici in suo possesso? Anche questo è difficile: in 400 anni, con tutte le persone che hanno provato a risolvere il problema, qualcuno l'avrebbe trovata!
L'ipotesi più accreditata è che Fermat avesse una dimostrazione, ma che questa contenesse un errore. Errore di cui, forse, anche lui si era accorto (ma dopo la famosa annotazione a margine di pagina): questo spiegherebbe perché non l'abbia mai pubblicata o scritta a nessuno, neanche quando poi ha reso nota la sua dimostrazione nel caso particolare in cui n=4.
Ma c'è una terza ipotesi: e se Fermat avesse deciso di fare uno scherzo alle generazioni future? Se avesse scelto una congettura volutamente difficile, sperando che più persone possibile ci sbattessero la testa, cercando la sua dimostrazione, che in realtà non esisteva?
Per quanto mi riguarda, mi piace immaginare Fermat nel suo studio, la scrivania piena di fogli, i mobili di legno massiccio, le nuvole fuori dalla finestra; una copia della Commedia di Dante poggiata sulla poltrona, aperta all'ultima pagina del Purgatorio; e lui che scrive con una penna d'oca quell'annotazione a margine, mentre se la ride.
Oggi è il 14 marzo, il giorno del Pi Greco!
Il Pi Greco è probabilmente la costante matematica più conosciuta, quel numero che si nasconde nel cerchio e da vita a numerose competizioni per ricordarne le cifre.
Vuoi saperne di più? Qui trovi il mio post di qualche anno fa.
Buon Pi Day!




Battaglia Navale era il quinto schema del Trofeo della Logica Apuana, e uno dei più difficili: solo cinque squadre hanno provato a risolverlo, e solo una c'è riuscita!
Qui trovi le regole.
(Se non vedi la nave nell'immagine sopra o nelle seguenti, prova a ricaricare la pagina)
La prima cosa da fare quando si prova a risolvere uno schema di Battaglia Navale è segnare con una X tutte le caselle in una riga o colonna con uno 0 (in questo schema non ce ne sono), e le caselle vicine ad un pezzo di nave già inserito, poiché due navi non possono toccarsi tra di loro.
Segniamo con un rombo le caselle in cui sappiamo che dovrà esserci una nave (in questo caso, perché il pezzo di nave data deve continuare verso il basso) ma non sappiamo che forma abbia (in questo caso, potrebbe essere lunga 2, 3 o 4).
Guardiamo ora la prima colonna: ha solo sette caselle vuote, e ben sei devono contenere una nave!
Proviamo a vedere se la prima casella in alto può essere vuota: in tal caso la colonna sarebbe formata da due navi da 3:
Se ora disegnassimo tutte le X corrispondenti, ci accorgeremmo che occupano l'intera seconda colonna, in cui però deve trovarsi una nave.
Allora la prima casella della prima colonna non può essere vuota, e possiamo quindi disegnarci una nave. Allo stesso modo possiamo escludere altre tre caselle dall'essere vuote:
Ricordiamoci che due navi non possono toccarsi nemmeno in diagonale: questo ci consente di mettere un po' di X. Inoltre nella prima riga ci deve essere solo una nave, quindi tutto il resto deve essere vuoto.
Guardiamo ora la quarta colonna, quella con un 5: abbiamo ancora solo sei caselle da decidere. Se supponiamo che la prima in alto sia vuota, abbiamo un problema con la colonna del 2 a sinistra, proprio come prima facevamo con le prime due colonne. In modo simile possiamo escludere altre tre caselle dall'essere vuote:
Mettiamo le X in diagonale alle navi, e nella sesta riga, quella del 2, che è piena.
Notiamo che questo ci consente di concludere la nave che avevamo a metà.
Ora la colonna del 5 ha sicuramente una nave da 3 e due navi singole (che però potrebbero continuare in orizzontale!). La domanda è: la nave da 3 si trova sopra o sotto?
Se fosse sopra, la colonna del 2 non potrebbe essere completata. Quindi deve essere sotto. Mentre le due navi del 2 devono essere sopra.
Ora la riga del 4 è finita. Possiamo concludere la nave da 2 e mettere alcune X in giro:
Mettiamo una nave nell'ultima casella rimasta della seconda colonna. Possiamo poi concludere la prima colonna.
Notiamo che abbiamo già inserito tutte e tre le navi da 2, e anche quella da 4. Allora la nave nella seconda riga non può che essere una nave da 3.
Ora ci mancano solo da inserire tre navi da 1. Nella penultima riga dobbiamo metterne due, e l'ultima andrà nella seconda riga per completare l'ultima colonna.