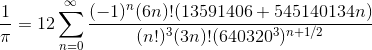Merry Christmas!

🎄

Classifica C(VD)ampionato

Il C^VDampionato si è concluso.
Questi i migliori cinque classificati:

Posizione	Nickname	Punteggio
1	Arianna Domenichelli	100
2	Daniel Zambanini	73
3	Ilaria Doemichelli	46
4	Yi Ying Ye	42
5	Niccolò Benassi	39

La gara non era affatto semplice, come dimostrano i punteggi. Nonostante questo Arianna è riuscita a risolvere correttamente tutti gli schemi. Complimenti a lei e anche a tutti gli altri partecipanti!

A breve i partecipanti che hanno inserito la propria mail riceveranno un messaggio con il dettaglio del proprio punteggio.

Fine C(VD)ampionato

Il primo C^VDampionato si è concluso.

Grazie a tutti per aver partecipato!

A breve saranno pubblicati i risultati. Nel frattempo ecco le soluzioni:


Si ringraziano Alberto Fabris e Giorgio Dendi per l'aiuto nella preparazione della gara.

C(VD)ampionato

Inizia il C^VDampionato!
Qualche ultimo consiglio e chiarimento:

• I punteggi dei vari schemi sono indicati a fianco del nome.
• Punteggi più alti indicano giochi più difficili.
• Yin Yang e Percorso a Pois hanno soluzione unica solo se considerati insieme.
• Gli schemi non sono facili e il tempo è poco: forse è bene cominciare dai giochi che sai fare meglio o da quelli più semplici.
• Non sottovalutare l'inserimento delle risposte! Quando hai completato uno schema inserisci subito la sua soluzione nel modulo.

Scarica il testo di gara.

Visualizza il testo di gara sul tuo browser.

Visualizza il modulo per l'inserimento delle risposte in un'altra pagina.

Modulo per l'inserimento delle  risposte:

Buona fortuna a tutti!

Manca poco

Manca poco più di un giorno all'inizio del C^VDampionato!
Assicurati di aver letto il regolamento e le altre informazioni sulla gara.
Puoi esercitarti con alcuni dei giochi anche su questo blog: li trovi nella pagina "Giochi Logici".
Il testo della gara verrà pubblicato alle 15.00 di domani.

Halloween matematico

E' Halloween! 👻😈💀 Streghe, mostri, scheletri, vampiri, fantasmi... Tutti costumi scontati... se stai cercando un'idea originale potresti travestirti da Versiera.

La Versiera è il costume perfetto per Halloween se vuoi mostrare la tua cultura matematica.

La Versiera è una curva del piano: a studiarla in dettaglio e a darle il suo nome fu Maria Gaetana Agnesi, matematica italiana. 

Quando il testo in cui ne parlava (Istituzioni analitiche ad uso della gioventù italiana) fu tradotto in inglese il nome "versiera" fu inteso come abbreviazione di "avversiera", ovvero "strega", "avversaria di Dio". Per questo la curva è conosciuta in lingua inglese come "witch of Agnesi".

La sua equazione:

Costruisci la tua maschera: scarica o visualizza nel browser l'immagine, stampala su un cartoncino e ritagliala.

Qualche parola su Maria Gaetana Agnesi

Nasce nel 1718 e muore nel 1799 a Milano. Appartiene ad una famiglia agiata e il padre (cosa assai rara) la incoraggia nello studio delle lingue (arriverà a parlarne sette) e delle scienze, tra cui la matematica.

Vuole diventare monaca ma il padre si oppone, così rimane in casa ad accudire lui ed i fratelli. Le viene offerta una cattedra all'Università di Bologna, che rifiuta.

Successivamente smette di interessarsi alle scienze e si dedica alla cura delle donne malate e alla religione.

E' considerata una tra le più importanti matematiche e nel 2014 Google le dedica un doodle.

Parabole e sorrisi

Oggi venerdì 5 ottobre 2018 è la giornata mondiale del sorriso. 😃
E quale giorno migliore di questo per parlare di parabole?
Le parabole, infatti, con quella loro forma tondeggiante sono perfette per rappresentare una bocca sorridente:

Le parabole, algebricamente, sono equazioni di secondo grado (con variabile, solitamente, x): il grafico di una parabola dipende quindi da tre numeri, i suoi coefficienti: a, b e c.
L'equazione di una parabola è:

La parabola della prima immagine qui sopra ha equazione y=x², quindi con a=1, b=0 e c=0. Puoi cambiare a piacimento i valori di a, b e c, ottenendo tante parabole che daranno vita a tanti sorrisi:

Devi però fare attenzione a quali numeri scegli... Se a è negativo, infatti, potresti trovarti davanti ad una brutta sorpresa:

Torniamo alla nostra prima parabola. Il nostro nuovo amico sembra davvero simpatico. Ha un sorriso enorme:

Davvero enorme:

Forse addirittura troppo... Abbiamo dimenticato che la parabola continua all'infinito... Che non sia il miglior modo matematico per rappresentare un sorriso? 😕
Potremmo provare con un semicerchio (ovviamente utilizzando la parte giusta... Non vogliamo avere altre facce tristi!):

Eppure non possiamo abbandonare il nostro amico al suo enorme destino... Deve esserci qualcosa che possiamo fare!
Cominciamo con il chiederci perché il semicerchio è diverso.
La sua equazione è:

Per alcune x questa funzione non esiste! Ad esempio, con x=-3 dovremmo calcolare la radice quadrata di 1-9=-8, ma -8 è un numero negativo, dunque la sua radice non esiste (almeno non nei numeri reali)! La stessa cosa succede con x=2: 1-4=-3.
Ecco perché vediamo il semicerchio soltanto con x tra -1 e 1: perché per gli altri valori semplicemente il semicerchio non esiste.
Quello che ci serve è quindi "costringere" la funzione a "non lavorare" per alcune x: ad esempio potremmo volere che la parabola esista soltanto per x tra -2 e 2.
Le radici quadrate sono un ottimo metodo per risolvere problemi del genere: se nell'equazione della parabola compare la radice allora la parabola non esisterà per x tra -2 e 2.
Aggiungendo soltanto quella radice, però, la parabola assume una forma strana:

Questo perché la radice non modifica soltanto per quali x la funzione esiste, ma anche che valore assume! Ma niente paura: per far tornare la bocca del nostro amico ad un bel sorriso ci basta dividere per la stessa radice:

Buona giornata mondiale del sorriso a tutti! 😄

Percorso a Pois

Percorso a Pois fa parte dei giochi del Campionato Studentesco di Giochi Logici.

Disegna un percorso chiuso che passi per tutte le caselle dello schema, orizzontalmente o verticalmente, e che non si tocchi né si incroci. Nelle caselle con un cerchio nero il percorso compie un angolo di 90°, nelle caselle con un cerchio bianco il percorso passa dritto.

Clicca la bandiera verde, poi un numero da 1 a 6 per cominciare a giocare:

Scuola guida per matematici: Attenzione Fattoriali Vaganti

Uscendo di casa è facile incontrare cartelli stradali.

E i cartelli stradali hanno un legame con la matematica: come in questa disciplina si utilizzano +, -, ∑, ⊥, ⇒..., così anche la segnaletica stradale serve per comunicare velocemente e brevemente con gli altri.

A volte, però, il significato matematico dei segnali non è lo stesso che i comuni utenti della strada gli attribuiscono. Ad esempio...

Attenzione: fattoriali vaganti

Il cartello indica la possibile presenza sulla strada di fattoriali vaganti. E' necessario rallentare e prestare particolare attenzione: se si viene colpiti infatti la propria massa aumenta più che esponenzialmente, causando gravi pericoli per gli altri utenti. A meno che non siate 1 o 2, ovviamente.

Non sai cosa sono i fattoriali? Ecco una breve spiegazione: 

Il fattoriale del numero n è il prodotto di tutti i numeri naturali da 1 a n e si indica con n!. Ad esempio:

• 1! = 1
• 2! = 1 x 2
• 5! = 1 x 2 x 3 x 4 x 5
• 10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10

Formalmente:

I fattoriali crescono molto velocemente all'aumentare di n: infatti, se anche 2! = 2 e 4! = 24, già 10! = 3.628.800 e 15! = 1.307.674.368.000.

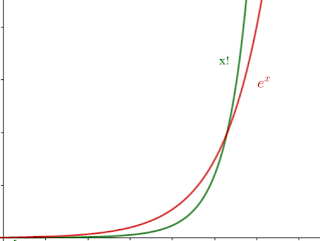Per x basse l'esponenziale è maggiore del fattoriale, ma per x alte il fattoriale cresce molto di più!

Per questo bisogna prestare attenzione: più si è grossi e più il fattoriale fa diventare grossi! Questo vale per tutti i numeri (se ve lo state chiedendo, anche con 0. Infatti 0! è definito uguale ad 1, e 1 è molto più grande di 0... infinitamente più grande!) tranne che per 1 e 2:

• 1! = 1
• 2! = 2

Scuola guida per matematici: Lezione successiva

Futoshiki

Futoshiki fa parte dei giochi del Campionato Studentesco di Giochi Logici.

In ogni casella devi scrivere un numero tra 1 ed N (dove N è la grandezza dello schema) in modo che:
- in ogni riga ci siano tutti i numeri da 1 a N una sola volta;
- in ogni colonna ci siano tutti i numeri da 1 a N una sola volta;
- i segni > e < siano rispettati.

Clicca sulla bandiera verde e poi su un numero da 1 a 6 per iniziare a giocare.

Repulsione

Repulsione fa parte dei giochi del Campionato Studentesco di Giochi Logici.

Inserisci un numero da 1 a 4 in ogni casella (quadrata o rettangolare) in modo che due numeri uguali non si tocchino né in orizzontale, né in verticale, né in diagonale.

Clicca sulla bandiera verde e poi su un numero da 1 a 6 per cominciare.

 

C(VD)ampionato - regolamento

Ecco il regolamento del C^VDampionato, che svela quali giochi saranno presenti.

Scarica il regolamento cliccando qui

Kropki

Kropki fa parte dei giochi del Campionato Studentesco di Giochi Logici.

In polacco "kropki" significa "puntini", e guardando uno schema non è difficile capire perché.

In ogni casella devi scrivere un numero da 1 a n (dove n è la grandezza dello schema) in modo che 

• in ogni riga e colonna compaiano una ed una sola volta tutti i numeri da 1 a n;
• tra due caselle contenenti numeri consecutivi si trovi (sempre!) un pallino bianco;
• tra due caselle contenenti numeri l'uno il doppio dell'altro si trovi (sempre!) un pallino nero.

In particolare, se tra due caselle non si trova nessun pallino questi numeri non sono né consecutivi né uno il doppio dell'altro. 

Inoltre tra 1 e 2 si può trovare indifferentemente sia un pallino bianco che uno nero.

Clicca sulla bandiera verde e scegli un numero da 1 a 6 per giocare.

Slalom

Slalom fa parte dei giochi del Campionato Studentesco di Giochi Logici.

Consiste in una griglia quadrata divisa in quadratini: in ogni quadratino deve essere disegnata una delle due diagonali (e soltanto una!), in modo che, a schema risolto:

• Da ogni numero presente partano esattamente quel numero di diagonali;
• Non ci siano regioni chiuse formate dalle diagonali (se una regione confina con il bordo dello schema non è chiusa).

Clicca sulla bandiera verde, poi scegli un numero da 1 a 6 per giocare.

Quinto Campionato Studentesco di Giochi Logici

Oggi 7 aprile 2018 a Modena si è tenuta la finale del Quinto Campionato Studentesco di Giochi Logici.
Massa Carrara è stata la provincia con più partecipanti ed ha portato in finale il maggior numero di studenti. Anche i risultati sono stati ottimi in tutte le sette categorie, nonostante il livello tecnico, anche a detta dell'organizzatore Alberto Frabris, si sia alzato in maniera notevole.

Primarie individuali

Vengono premiate due ragazze della provincia di Massa Carrara: Veronica Lucia, arrivata 11°, e Linda Babboni, con un ottimo quarto posto.

Medie individuali

Dopo il titolo nazionale vinto gli ultimi due anni da Arianna Domenichelli (quest'anno nel biennio), ben cinque nostri partecipanti vengono premiati, tutti dalla scuola media Buonarroti: Michelle Ducci (13°), Claudia Dazzi (11°), Sebastian Furlan (10°), Niccolò Consigli (9°) e Giulia Massa (8°).

Biennio individuali

In questa categoria, in cui nessuno ha finito tutti i problemi, non riusciamo a guadagnare il titolo: due ottimi posti sono comunque raggiunti da Niccolò Benassi, quarto, e Arianna Domenichelli, addirittura seconda.

Triennio individuali

Giorgia Benassi riesce a riconquistare il titolo vinto l'anno scorso, nonostante l'errore fatto nel gioco a sorpresa (Attrazione Atomica), in cui ha dimenticato di annerire una casella, davanti a ben tre ragazzi del Liceo Copernico di Udine.

Medie a squadre

Ottimo risultato della squadra "I numeri primi", con Leonardo Martini, Sebastian Furlan, Niccolò Consigli e Nicola Cavalieri, che arrivano secondi. Vengono battuti soltanto da una squadra composta da solo due persone... a cui Fabris riserva ovviamente molti complimenti.

Biennio a squadre

Ben due squadre premiate in questa categoria: i "Prodotti notevoli" (Vittoria Franzini, Irene Lucetti, Matteo Redi e Giulio Mazza) arrivano settimi, mentre vincono il titolo, partendo da favoriti, i "Superfariakaristichelabirintoso" (Arianna Domenichelli, Avio Baccioli, Niccolò Benassi, Elisa Sabadini).
Da sottolineare il fatto che dalla nostra provincia quest'anno sono passate in finale ben due squadre di un professionale, le prime in assoluto a qualificarsi in Italia. Una di queste, i "Super" (Alice Giorgi, Rebecca Gabelloni, Chiara Gaudino e Mattia Dani), arriva 9°, a poca distanza dai premiati.

Triennio a squadre

L'intera gara, come dice Fabris, è piena di sorprese. In questa categoria due squadre partivano da favorite: una delle due non viene nemmeno premiata, l'altra sono i "Poker d'assi cartesiani" (Giorgia Benassi, Gregorio Vietina, Ilaria Domenichelli, Daniele Bugliani), che arrivano "soltanto" sesti, senza riuscire a confermare il titolo vinto lo scorso anno.

Gara degli insegnanti

Anche se non è una competizione ufficiale, nella squadra vincitrice, creata sul momento, c'è anche il professor Riccardo Bellè del Liceo Fermi di Massa.

Qualche giorno dopo...

Nella categoria delle medie a squadre "I fantastici 4" (Giada Baruffi, Claudia Dazzi, Giorgia Galli e Emanuele Rabasco) arrivano terzi ma al loro posto vengono premiati, per un problema di omonimia, i trentini "I fantastici 4". Il loro vero risultato viene comunicato solo qualche giorno dopo la finale.

Hashiwokakero

Per gli amici Hashi, viene anche chiamato semplicemente "Ponti". Nel Campionato Studentesco di Giochi Logici compaiono anche schemi di questo gioco.

Nel mare ci sono diverse isole (rappresentate da cerchi) collegate tra di loro da ponti verticali o orizzontali:

• i ponti non si incrociano a vicenda, 
• il numero sopra ogni isola indica quanti ponti partono da lì, 
• due isole sono collegate da uno o due ponti (non tre o più). 

A schema risolto deve essere possibile arrivare da ogni isola ad ogni altra solo passando per i ponti, ovvero non possono esserci gruppi isolati di isole.

Clicca sulla bandiera verde per cominciare, poi scegli un numero da uno a sei e prova a completare gli schemi!

Il gioco dei dolcetti (ovvero un'introduzione alla teoria dei giochi)

Giga sta cercando qualcuno che giochi con lui, forse tu sei la persona giusta!

Ci sono alcuni dolcetti (più di cinque ma meno di 31, per l'esattezza), e a turno ne prenderete un numero tra 1 e 4, a vostra scelta. L'ultimo dolcetto è avvelenato... chi lo prende perde!

Attento, però, perché Giga non gioca a caso... segue una strategia!
Ecco perché sembra vincere sempre, qualunque cosa tu faccia! 😔
Ma niente paura, anche tu puoi imparare la sua strategia... Una strategia vincente, che ti eviterà per sempre la sconfitta e che potrai sfruttare giocando contro i tuoi amici... 😉 Sei pronto?
Clicca la bandiera verde per cominciare a giocare... e buona fortuna!



Serve aiuto per trovare la strategia?

Suggerimento 1  

Vedi quel pulsante rosso sulla destra...? Forse succederà qualcosa che potrebbe aiutarti nella ricerca della strategia cliccandoci sopra.

Suggerimento 2  

Prenditi una pausa dal gioco e prova a ragionare dall'ultima mossa... Se davanti hai un solo dolcetto, sarai costretto a prendere quello e perderai... Se hai davanti due dolcetti, puoi prenderne uno e lasciare l'altro a Giga, così vincerai... E con 3 dolcetti? E con 30?

Come trovare una strategia vincente?  

Tutti i tuoi tentativi di trovare la strategia sono stati vani? Niente paura, ti aiuto io.

Come scritto nel secondo suggerimento, se ti trovi davanti un solo dolcetto hai perso. Diciamo che 1 dolcetto è una situazione perdente perché qualunque mossa tu faccia vincerà Giga.
Se hai davanti due dolcetti, al contrario, puoi prenderne uno e lasciare l'ultimo a Giga. Diciamo che 2 dolcetti è una situazione vincente perché puoi lasciare il tuo avversario in una situazione perdente.
Anche se hai davanti tre dolcetti puoi prenderne due e lasciare l'ultimo a Giga. 3 dolcetti è una situazione vincente.
Se hai davanti quattro dolcetti puoi prenderne tre e lasciare l'ultimo a Giga. 4 dolcetti è una situazione vincente.
Se hai davanti cinque dolcetti puoi prenderne quattro e lasciare l'ultimo a Giga. 5 dolcetti è una situazione vincente.
Se hai sei dolcetti, però, qualunque cosa tu faccia lascerai Giga in una situazione vincente. Quindi 6 dolcetti è una situazione perdente.
Se hai sette, otto, nove o dieci dolcetti, puoi lasciarne sei a Giga, quindi 7, 8, 9 e 10 dolcetti è una situazione vincente.
11, invece, è una situazione perdente perché qualunque cosa tu faccia lascerai a Giga una situazione vincente.

Ti sei accorto di quello che sta succedendo? Abbiamo una situazione perdente seguita da quattro situazioni vincenti, poi una situazione perdente seguita da quattro vincenti e così via. Così, se verde è vincente e rosso perdente:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 ...

Possiamo quindi notare che, se cominciamo a giocare con 6, 11, 16, 21, 26 dolcetti, perderemo! In questo caso ci conviene far iniziare Giga. Se invece iniziamo con un altro numero di dolcetti, dovremo cominciare noi, e lasciare a Giga un numero perdente di dolcetti!

Grazie, ma... Quindi tutte le volte che giochiamo dobbiamo scriverci i numeri, e colorarli di verde o di rosso? Non c'è un modo più veloce per sapere quanti dolcetti dobbiamo prendere? Effettivamente sì, c'è.
Come fare?  

Per vederlo, proviamo a riscrivere i numeri sopra, ma senza contare tutti i dolcetti, bensì solo quelli non avvelenati (ovvero tutti quelli di prima tranne uno):

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 ...

Possiamo notare che i numeri rossi, ovvero perdenti, sono quelli multipli di 5! Perché proprio questo numero? La risposta non è troppo difficile: possiamo togliere un numero di dolcetti tra 1 e 4, quindi possiamo raggiungere i primi quattro numeri precedenti... Non il quinto! Infatti, i numeri rossi sono quelli che lasciano l'avversario sicuramente in un numero verde, quindi devono distare 4+1 l'uno dall'altro.
Per sapere in ogni momento quanti dolcetti dobbiamo prendere per vincere, basta contare quelli rimasti, sottrarre uno (quello avvelenato), e dividere per cinque. Se il resto che otteniamo è 0, significa che siamo in un numero rosso, e dunque non abbiamo la vittoria assicurata. Se il resto è 1, significa che dobbiamo prendere 1 dolcetto per lasciare al nostro avversario un numero rosso. Se il resto è 2, significa che dobbiamo prendere 2 dolcetti, e così via (facendo qualche partita, noterai che il numero di dolcetti che devi prendere è sempre 5 meno il numero di dolcetti che ha preso Giga: sai spiegarti il perché?).
Effettivamente, questa è proprio la strategia che usa Giga! Ecco un pezzo di codice del gioco creato in Scratch (puoi trovarlo qui):

"Numero di dolcetti" è il numero di dolcetti presenti. Il computer lo diminuisce di 1, lo divide per cinque e dice a Giga di prendere tanti dolcetti quanto il resto di questa divisione. Se il resto è 0, però, questo non è possibile: non può prendere 0 dolcetti! In questo caso, non ha una strategia vincente, quindi sceglierà un numero a caso tra 1 e 4 e prenderà quel numero di dolcetti.

Pi Day

Il 14 marzo è il compleanno di Wacław Sierpiński (1882, 1969), Karl Wilhelm Lorenz (1886, 1918) e Michael Berry (1941), oltre che del famoso Albert Einstein (1879, 1955), ma non è per questo che è un giorno importante.

E' perché il 14 marzo è il pi greco day (che non è, come alcuni potrebbero pensare, il giorno di Pippo Ignazio).

Pippo Ignazio, originario di Atene, anche detto P. I. Greco.

Il pi greco è definito come il rapporto tra la circonferenza e il diametro di un cerchio. E' un numero decimale infinito. Non solo, è perfino irrazionale, nonché trascendente (cosa che rende impossibile la quadratura del cerchio, ma questa è un'altra storia).

Approfondimento a fine pagina: Numeri decimali e irrazionali  
Approfondimento a fine pagina: Numeri trascendenti  

Il pi greco day si festeggia il 14 marzo perché equivale a (circa) 3,14, che è proprio questa data scritta all'inglese "mese, giorno".

Certo, vista l'importanza che pi greco sembra avere (ha persino un giorno a lui dedicato!), viene da chiedersi quanto valga, quindi, pi greco.

Abbiamo detto che ha infinite cifre dopo la virgola, e che non si ripetono mai, ma quali sono queste cifre esattamente?

Qualcuno lo approssima a 22/7 (ovvero 3,142857 142857...), altri a 355/113 (ovvero 3,141592...), ma ovviamente nessuno di questi due numeri è esattamente pi greco.

Il fatto è che nessuno sa (né saprà mai) quanto vale pi greco esattamente.

Oh, sappiamo tante cose su di lui.

Sappiamo che la sequenza 0123456789 si trova al 17.387.594.880 decimale, ad esempio.

Sappiamo le sue prime 2 000.000.000.000.000 cifre (e anche oltre).

Approfondimento a fine pagina: Pi greco e approssimazione  

Sappiamo anche come possiamo calcolare pi greco. All'inizio, questo conto veniva eseguito disegnando poligoni con un numero di lati molto alto, e che dunque approssimavano la circonferenza. Nel corso della storia, invece, i matematici hanno trovato diverse somme infinite uguali a pi greco (ovvero: se potessimo calcolare la somma di un numero infinito di addendi, otterremmo precisamente pi greco. Ma questo, per ovvie ragioni, ci è impossibile).

Una delle più complicate è probabilmente quella dei fratelli Chudnovsky:

Approfondimento a fine pagina: Calcolare questa sommatoria  

E' bello poter calcolare pi greco... Ma non sono certo calcoli semplici! Per questo la ricerca di nuove cifre di questo numero, che ha destato interesse fin dall'antica Grecia, ha avuto un importante sviluppo con l'avvento dei computer. Si è passati da 1.120 cifre calcolate nel 1949 a più di 2.600.000.000.000 cifre calcolate nel 2010.

Eppure, non sappiamo tutto di pi greco. Non si è ancora riusciti a dimostrare, nonostante si suppone che sia vero, se pi greco sia un numero normale, né se sia un numero-universo.

Approfondimento a fine pagina: Numeri normali e numeri-universo 

Resta comunque un'altra domanda da porsi su pi greco: perché è così famoso?
E' la costante matematica più citata, e chiunque, anche se non è un esperto, sa che è circa 3,14.
Ci sono persone che compongono odi o cucinano torte in suo onore; c'è chi ha speso una vita per calcolare le sue cifre, e chi le impara a memoria.
C'è persino un giorno dedicato a lui!
Ma perché?

Forse perché è allo stesso tempo un numero così semplice (se ne parla in quinta elementare) e così complicato (vi ricordate la sommatoria...?), nonché pieno di segreti.
Se si riuscisse a dimostrare che pi greco è normale e universale, se si trovasse una formula che permette di comprendere tutte le cifre di pi greco con pochi, semplici simboli, perderebbe il suo fascino? Oppure diventerebbe ancora più famoso?

Quanta bellezza in un rapporto così semplice come quello tra circonferenza e diametro!

Approfondimento: numeri decimali, irrazionali, trascendenti

Numeri decimali e irrazionali Un numero decimale è un numero che si scrive utilizzando la virgola. Ad esempio, sono decimali 2,5 e 0,0007.

Un numero decimale può essere infinito se la sua rappresentazione decimale precisa è formata da infinite cifre dopo la virgola (ad esempio 1/3=0,33333...).

I numeri decimali infiniti possono essere periodici (ovvero le cifre si ripetono. Ad esempio 0,333... o 0,12 567 567 567...) oppure irrazionali (ovvero che non si possono scrivere come frazioni). Le cifre dopo la virgola dei numeri irrazionali, oltre ad essere infinite, non si ripetono con uno schema preciso. Ad esempio, radice di 2 è irrazionale.

Numeri trascendenti I numeri trascendenti sono numeri irrazionali che non possono essere espressi come soluzione di un'equazione a coefficienti razionali (i numeri razionali sono gli interi e le frazioni, anche negativi).

Radice di 2 non è trascendente, poiché è soluzione dell'equazione x²=2. Tutte le radici (e somme o differenze di radici) sono numeri non trascendenti. Al contrario, per quanto proviate, non riuscirete mai a trovare un'equazione a coefficienti razionali che ha come soluzione pi greco.

Curiosi di sapere altri numeri trascendenti? Il più famoso, dopo pi greco, è il numero di Nepero: e. Sono trascendenti anche e^ℼ e uno tra e+ℼ e exℼ, anche se non si sa quale.

Approfondimento: approssimazione, sommatorie, numeri normali e numeri-universo

Pi greco e approssimazione 2 000.000.000.000.000 (o 2x10¹⁵) può sembrare solo un numero di 16 cifre (e cosa vuoi che sia 16?), ma in realtà è enorme. Solo per dare l'idea, se volessimo calcolare la circonferenza massima dell'universo visibile (supponendo che sia sferico e di conoscerne il raggio) con un'approssimazione minore del raggio di un atomo, ci basterebbero le prime 40 cifre.
2 000.000.000.000.000 è un numero 100.000.000.000.000 maggiore di 40.

Calcolare questa sommatoria Cerchiamo ora di capire, almeno approssimativamente, che cosa significano i simboli qui sopra.

Per prima cosa, forse non sai che n!, che si legge "enne fattoriale", indica il prodotto di tutti i numeri da 1 a n. Quindi 1!=1, 2!=1x2=2, 5!=1x2x3x4x5=120, 10!=3.628.800. E' facile intuire che, se il numero n è grande, n! è molto grande. Pensa quindi quanto può diventare enorme (6xn)! quando n è solo "poco" grande.

Un'altra cosa che devi sapere è il significato del simbolo ∑, ovvero sommatoria. Significa che devi prima prendere n=0 (come scritto sotto) e calcolare quella frazione sostituendo n=0. Poi aumenti n di 1, e calcoli quella frazione sostituendo n=1. Poi aumenti n di 1, e calcoli quella frazione sostituendo n=2. E così via, fino ad arrivare ad infinito (come scritto sopra). Una volta che hai calcolato tutte le frazioni con tutti i valori di n, le sommi tra di loro (infatti è una sommatoria). Ovviamente non possiamo calcolare le frazioni per tutti gli n (perché sono infiniti). Più valori calcoliamo, e più quel numero si avvicina a 1/𝝅 (infatti all'inizio della frazione compare (-1)ⁿ , che è positivo per n pari e negativo per n dispari. Vuol dire che la frazione con n=0 sarà positiva, con n=1 negativa e così via. Aggiungendo e togliendo, piano piano ci avviciniamo alla meta). Facciamo un esempio. Per n=0 ottengo 0,0265258179936665073198830567197... Per n=1 ottengo -4,98422492211907170652852338404... x 10^-16  Sommandoli ottengo 0,02652581799366600889739084481253... Moltiplicando per 12 ottengo 0,31830981592399210676869013775035... Questo valore equivale a 1/𝝅.  Quindi 𝝅 = 3,1415933470263634335956928968...  Ci è bastato calcolare due frazioni per ottenere un numero molto simile a 3,1415926535897932384626433... ma non sono affatto stati conti semplici!

Numeri normali e numeri-universo I numeri "normali" in base 10 sono numeri irrazionali in cui tutte le cifre compaiono con la stessa frequenza nel suo sviluppo in base 10, così come le coppie di cifre (00, 01, ... 98, 99), le triple (000, 001, ... 998, 999), ecc.

I "numeri-universo" in base 10 sono numeri che nel loro sviluppo contengono qualunque sequenza immaginabile. Ad esempio, contengono la mia data di nascita, il tuo numero di cellulare e la sequenza di 1 e 0 con cui è salvato questo intero blog.

Link

Ecco qualche link che potrebbe interessarti se ti è piaciuto questo blog:

A proposito di Giochi Logici

• puzzlefountain.com : ovvero il sito dei Campionati Studenteschi di Giochi Logici. Potete trovare le regole di tutti i giochi dei Campionati, oltre ad ulteriori informazioni e ai testi delle finali delle scorse edizioni.
• Antelacus : il canale Twitch e il canale YouTube di Alberto Fabris, l'organizzatore dei Campionati Studenteschi. Parla di scacchi e giochi logici.
• PuzzlePicnic : un sito contenente una raccolta di schemi di diversi giochi logici, risolvibili sul computer.
• 100 Logic Games : un'applicazione gratuita contenente diversi giochi logici, molti dei quali presenti anche nei Campionati Studenteschi.

Gare di Giochi Logici on-line

• Puzzle Fountain : il sito dei Campionati Studenteschi, ogni tanto organizza anche tornei on-line.

I siti seguenti non sono italiani. Con o senza regolarità organizzano gare on-line a cui chiunque può partecipare; la difficoltà è spesso più alta di quella dei Campionati Studenteschi:

• gp.worldpuzzle.org : il sito del World Puzzle Grand Prix (e anche del World Sudoku Grand Prix): sono 8 round, uno ogni mese, e i migliori disputano la finalissima ai mondiali di Sudoku e Puzzle.
• wpc.puzzles.com : il sito degli USA.
• ukpuzzles.org : il sito del Regno Unito.
• logic-masters.de : il sito della Germania (che ha il difetto di non disporre sempre di un'adeguata traduzione in inglese).
• logicmastersindia.com : il sito dell'India.

Altri siti

• giorgiodendi.com : il sito del simpaticissimo Giorgio Dendi, che, oltre ad essere il creatore di Alberi, pubblica giochi di enigmistica e con le targhe.
• BASE Cinque : un sito con "appunti di matematica ricreativa".

Yin Yang

Gli schemi di Yin Yang fanno parte del Campionato Studentesco di Giochi Logici.

Posiziona in ogni casella un cerchio bianco o nero in modo che non siano presenti aree 2x2 dello stesso colore. A fine schema, tutte le caselle contenenti un cerchio bianco devono essere collegate tra di loro (verticalmente o orizzontalmente), così come le caselle contenenti un cerchio nero.
1. Clicca due volte la bandiera verde e passa allo schermo intero per vedere meglio.
2. Clicca un numero da 1 a 6 per scegliere lo schema.
3. Clicca su una casella per posizionare un cerchio nero, clicca un'altra volta per posizionare un cerchio bianco.
4. Quando hai finito clicca sulla "v" verde per controllare la tua soluzione.

Percorso Puntato

Gli schemi di Percorso Puntato fanno parte del Campionato Studentesco di Giochi Logici.

Devi disegnare nella griglia un percorso chiuso unendo i punti adiacenti in orizzontale o verticale. Il percorso deve passare da tutti i punti e non può incrociarsi.

1. Clicca la bandiera verde.
2. Clicca un numero da 1 a 6 per scegliere lo schema. (Gli schemi NON sono in ordine di difficoltà, e lo schema 6 è moooolto difficile 😁)
3. Clicca sugli spazi tra due punti una volta per sbarrarli e due volte per annerirli.
4. Quando hai finito clicca su "soluzioni"

Vasi comunicanti

Vasi Comunicanti è apparso per la prima volta nella finale nazionale individuale del Campionato Studentesco di Giochi Logici del 2017, come gioco a sorpresa.

Nello schema sono presenti dei vasi che devono essere riempiti, del tutto, in parte o per niente, di acqua (una casella deve però essere completamente piena oppure vuota, e caselle sulla stessa riga appartenenti allo stesso vaso non possono essere una piena ed una vuota). I numeri all'esterno indicano quante caselle, in quella riga o in quella colonna, sono piene d'acqua.

Clicca sulla bandiera verde e segui le istruzioni per imparare qualche trucco:


Se non hai mai visto Vasi Comunicanti e non capisci bene come riempire i vasi, divertiti a riempirne qualcuno (cliccando sul rubinetto in alto) in questo gioco:

Grattacieli

Grattacieli fa parte dei giochi presenti nel Campionato Studentesco di Giochi Logici.
In inglese viene chiamato Skyscrapers.

In una città di pianta quadrata ci sono grattacieli di diversa altezza. In ogni riga e in ogni colonna non ci sono grattacieli con la stessa altezza. I numeri esterni indicano quanti grattacieli si vedono da quel punto. I grattacieli più alti coprono quelli più bassi.

Clicca sulla bandiera verde per cominciare a giocare, e segui le iscrizioni per completare, passo passo, il tuo primo schema di Grattacieli!

 

Kakuro

Kakuro fa parte dei giochi presenti nel Campionato Studentesco di Giochi Logici.

Clicca su una casella per inserire un numero da 1 a 9. La somma dei numeri in un blocco di caselle bianche deve essere uguale al numero posto sopra (per i blocchi verticali) o a sinistra (per i blocchi orizzontali). In un blocco i numeri devono essere tutti diversi.

1. Clicca due volte la bandiera verde e passa allo schermo intero per vedere meglio.
2. Clicca un numero da 1 a 6 per scegliere lo schema. (Gli schemi NON sono in ordine di difficoltà)
3. Clicca su una casella e poi premi un numero sulla tastiera per inserire quel numero in quella casella. Se premi 0 la casella resta vuota.
4. Quando hai finito clicca su "soluzioni"

SUGGERIMENTO
Osserva i blocchi più piccoli e sfrutta le combinazioni uniche, riportate in una tabella che appare se clicchi sul pulsante "combinazioni uniche"

Sudoku

Sudoku è forse il gioco logico più conosciuto. Anch'esso si trova tra i giochi del Campionato Studentesco di Giochi Logici.

Tralascio le spiegazioni (che comunque potrete trovare all'interno del gioco) poiché è probabile che già le conosciate.

Cliccate sulla bandiera verde per cominciare.

Buon divertimento!

Serpente

Serpente è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.
In inglese viene chiamato Snake.

Prova la nuova versione, con due nuovi schemi, qui.

Clicca su una casella per inserire un numero o una x. 

Nella griglia si trova un serpente, del quale vengono indicate (con il numero 1 e un altro numero testa e coda. I numeri esterni indicano quante caselle in quella riga o colonna sono occupate dal serpente. Il serpente non può toccare o incrociare se stesso.

1. Clicca due volte la bandiera verde e passa allo schermo intero per vedere meglio.

2. Clicca un numero da 1 a 6 per scegliere lo schema.

3. Clicca su una casella e poi digita un numero sulla tastiera per inserire quel numero in quella casella. Se premi x nella casella compare una x ( puoi usarla per segnare che in quella casella non c'è nessun numero.

4. Quando hai finito clicca sulla "v" verde per controllare la tua soluzione. Se non riesci a risolvere lo schema clicca sul "?" rosso.

Campo Minato

Campo Minato è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.
Molto simile al gioco per computer Prato Fiorito; in inglese viene chiamato Minesweeper.

Clicca su una casella per sbarrare la casella. Clicca un'altra volta per mettere una mina.
Nella griglia sono posizionate alcune mine, e tu devi capire dove si trovano. I numeri indicano quante mine  hanno intorno (anche in diagonale).
Il numero sopra lo schema indica quante mine si trovano nello schema.
1. Clicca due volte la bandiera verde e passa allo schermo intero per vedere meglio.
2. Clicca un numero da 1 a 6 per scegliere lo schema.
3. Clicca una volta su una casella per mettere una barra (per segnalare che lì non c'è una mina) e due volte per mettere una mina.
4. Quando hai finito clicca sulla "v" verde per controllare la tua soluzione. Se non riesci a risolvere lo schema clicca sul "?" rosso.

Battaglia Navale

Battaglia Navale è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.
In inglese viene chiamato Battleship.

Nella griglia si nasconde una flotta di navi che tu devi trovare. La flotta è composta da:
 - 1 portaerei 4x1
 - 2 incrociatori 3x1
 - 3 bombardieri 2x1
 - 4 sottomarini 1x1
Due navi (o sottomarini) non possono toccarsi, nemmeno diagonalmente, e i numeri esterni indicano quante caselle sono occupate da navi (o sottomarini) in quella riga o colonna.
1. Clicca la bandiera verde.
2. Clicca un numero da 1 a 6 per scegliere lo schema.
3. Clicca una volta su una casella per inserire il mare (e segnalare che lì non c'è una nave). Se clicchi due volte compare un pallino (cioè un sottomarino). Le altre forme che compaiono servono per formare le navi più grandi.
4. Sul lato sinistro trovi una lista delle navi che devi inserire nella griglia: ogni volta che ne inserisci una clicca sul quadratino che ha di fianco per spuntarlo.
5. Non sai come proseguire? Clicca sulla faccina pensierosa a sinistra per iniziare un tentativo: le caselle che metterai saranno colorate di verde e spariranno non appena cliccherai "Chiudi tentativo".
6. Quando hai finito clicca sulla "v" verde per controllare la tua soluzione. Se non riesci a risolvere lo schema clicca sul "?" rosso.

Circuito Chiuso

Circuito Chiuso è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.
In inglese viene chiamato Slitherlink.

Disegna un circuito nella griglia unendo i punti adiacenti in orizzontale o verticale. Il circuito deve chiudersi su se stesso, non può incrociarsi e neppure sovrapporsi. I numeri indicano da quanti tratti sono circondati.

Clicca sulla bandiera verde per iniziare:

Problemi a risolvere gli schemi? Dà un'occhiata qui sotto per imparare qualche trucco 😉

Fari

Fari è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.

L'obiettivo è inserire delle navi (che sono disegnate come dei cerchietti neri)  in alcune caselle, in modo che:

• due caselle contenenti navi non si tocchino, nemmeno in diagonale;
• i fari (caselle con un numero all'interno) vedano (nella loro riga e nella loro colonna) tante navi quanto il numero che hanno sopra;
• una casella contenente un faro e una casella contenente una nave non si tocchino nemmeno in diagonale.

Clicca sulla bandiera verde per iniziare:

Piramide

Piramide è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.

L'obbiettivo è scrivere un numero da 1 a 9 in ogni casella in modo che ogni numero sia la somma oppure la differenza (in valore assoluto, quindi la differenza tra 3 e 4 è 1) dei due numeri sotto di lui. Inoltre, nelle righe grigie i numeri non possono ripetersi, mentre nelle righe bianche deve esserci almeno un numero che compare almeno due volte.

Clicca sulla bandiera verde per provare:

Alberi

Alberi è un gioco logico creato da Giorgio Dendi (visualizza il suo sito) e comparso su numerose riviste (una di queste è AmicoLogico).
Alberi è uno dei giochi presenti nelle gare dei Campionati Studenteschi di Giochi Logici.
Viene anche chiamato Stelle o Star Battle.

Lo scopo è inserire alcuni alberi nella griglia, in modo che:

• In ogni riga sia presente uno ed un solo albero;
• In ogni colonna sia presente uno ed un solo albero;
• In ogni podere (un'area colorata) sia presente uno ed un solo albero;
• Le caselle in cui si trovano due alberi non si tocchino tra loro, nemmeno in diagonale.

Prova a completare alcuni schemi (clicca sulla bandiera verde in alto a destra per cominciare. Da lì in poi, segui le istruzioni!).

Buon divertimento!

Problemi nel risolvere gli schemi? Dai un'occhiata qui sotto per imparare qualche trucco 😉